Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

[Mức độ 3] Một khối cầu được đặt trong nó một khối trụ sao cho khối cầu đi qua tất cả các hai đường tròn đáy của khối trụ. Gọi diện tích của khối cầu và diện tích xung quanh của hình trụ trên thứ tự là \(S,S’\); thể tích của khối cầu và khối trụ trên thứ tự là \(V,V’\). Biết tỷ số\(\frac{S}{{S’}} = 2\) Tính\(\frac{V}{{V’}}\)?

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

[Mức độ 3] Một khối cầu được đặt trong nó một khối trụ sao cho khối cầu đi qua tất cả các hai đường tròn đáy của khối trụ. Gọi diện tích của khối cầu và diện tích xung quanh của hình trụ trên thứ tự là \(S,S'\); thể tích của khối cầu và khối trụ trên thứ tự là \(V,V'\). Biết tỷ số\(\frac{S}{{S'}} = 2\) Tính\(\frac{V}{{V'}}\)? A.\(\frac{V}{{V'}} = \frac{3}{{2\sqrt 2 … [Đọc thêm...] về[Mức độ 3] Một khối cầu được đặt trong nó một khối trụ sao cho khối cầu đi qua tất cả các hai đường tròn đáy của khối trụ. Gọi diện tích của khối cầu và diện tích xung quanh của hình trụ trên thứ tự là \(S,S’\); thể tích của khối cầu và khối trụ trên thứ tự là \(V,V’\). Biết tỷ số\(\frac{S}{{S’}} = 2\) Tính\(\frac{V}{{V’}}\)?

[ Mức độ 2] Một khối trụ được đặt trong nó một khối cầu sao cho khối cầu tiếp xúc với tất cả các đường sinh của khối trụ đồng thời khối cầu đó tiếp xúc với hai đáy của khối trụ. Gọi thể tích của khối cầu và khối trụ trên thứ tự là \(V,V’\). Tính tỷ số\(\frac{V}{{V’}}\)?

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

[ Mức độ 2] Một khối trụ được đặt trong nó một khối cầu sao cho khối cầu tiếp xúc với tất cả các đường sinh của khối trụ đồng thời khối cầu đó tiếp xúc với hai đáy của khối trụ. Gọi thể tích của khối cầu và khối trụ trên thứ tự là \(V,V'\). Tính tỷ số\(\frac{V}{{V'}}\)? A.\(\frac{V}{{V'}} = \frac{3}{2}\). B.\(\frac{V}{{V'}} = \frac{3}{8}\). C. \(\frac{V}{{V'}} = … [Đọc thêm...] về[ Mức độ 2] Một khối trụ được đặt trong nó một khối cầu sao cho khối cầu tiếp xúc với tất cả các đường sinh của khối trụ đồng thời khối cầu đó tiếp xúc với hai đáy của khối trụ. Gọi thể tích của khối cầu và khối trụ trên thứ tự là \(V,V’\). Tính tỷ số\(\frac{V}{{V’}}\)?

[Mức độ 3] Cho hình chữ nhật \(ABCD\) có \(BC = 3AB\). Khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được khối trụ \(\left( {{T_1}} \right)\) có thể tích \({V_1}\); quay hình chữ nhật đó quanh cạnh \(BC\) ta được khối trụ \(\left( {{T_2}} \right)\) có thể tích \({V_2}\). Tỷ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

[Mức độ 3] Cho hình chữ nhật \(ABCD\) có \(BC = 3AB\). Khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được khối trụ \(\left( {{T_1}} \right)\) có thể tích \({V_1}\); quay hình chữ nhật đó quanh cạnh \(BC\) ta được khối trụ \(\left( {{T_2}} \right)\) có thể tích \({V_2}\). Tỷ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng A. \(3\). B. \(2\). C. \(\frac{3}{2}\). D. … [Đọc thêm...] về[Mức độ 3] Cho hình chữ nhật \(ABCD\) có \(BC = 3AB\). Khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được khối trụ \(\left( {{T_1}} \right)\) có thể tích \({V_1}\); quay hình chữ nhật đó quanh cạnh \(BC\) ta được khối trụ \(\left( {{T_2}} \right)\) có thể tích \({V_2}\). Tỷ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng

Để kỉ niệm 90 năm thành lập Đoàn TNCS Long Xuyên, đoàn trường THPT Long Xuyên tiến hành xây dựng một bồn hoa hình elip (như hình vẽ) gồm hai phần: Phần thứ nhất (có diện tích \({S_1}\)) giới hạn bởi hình elip và các đường parabol để trồng hoa; phần còn lại (có diện tích \({S_2}\)) để nuôi cá. Biết rằng tỷ số \(\frac{{{S_1}}}{{{S_2}}} = \frac{{a\pi + \sqrt 3 }}{{b\pi – \sqrt 3 }}\),\(a,b \in \mathbb{N}\). Tính \(a.b\).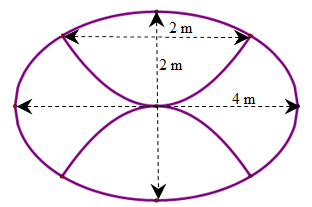

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:,

Câu hỏi: Để kỉ niệm 90 năm thành lập Đoàn TNCS Long Xuyên, đoàn trường THPT Long Xuyên tiến hành xây dựng một bồn hoa hình elip (như hình vẽ) gồm hai phần: Phần thứ nhất (có diện tích \({S_1}\)) giới hạn bởi hình elip và các đường parabol để trồng hoa; phần còn lại (có diện tích \({S_2}\)) để nuôi cá. Biết rằng tỷ số \(\frac{{{S_1}}}{{{S_2}}} = \frac{{a\pi + \sqrt 3 … [Đọc thêm...] vềĐể kỉ niệm 90 năm thành lập Đoàn TNCS Long Xuyên, đoàn trường THPT Long Xuyên tiến hành xây dựng một bồn hoa hình elip (như hình vẽ) gồm hai phần: Phần thứ nhất (có diện tích \({S_1}\)) giới hạn bởi hình elip và các đường parabol để trồng hoa; phần còn lại (có diện tích \({S_2}\)) để nuôi cá. Biết rằng tỷ số \(\frac{{{S_1}}}{{{S_2}}} = \frac{{a\pi + \sqrt 3 }}{{b\pi – \sqrt 3 }}\),\(a,b \in \mathbb{N}\). Tính \(a.b\).

(Chuyên Lê Quý Đôn – Điện Biên – 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M\) là trung điểm cạnh bên \(SC\). Gọi \(\left( P \right)\) là mặt phẳng chứa \(AM\) và song song với \(BD\), mặt phẳng \(\left( P \right)\) cắt \(SB,SD\) lần lượt tại \(B’\) và \(D’\). Tính tỷ số \(\frac{{{V_{S.AB’MD’}}}}{{{V_{S.ABCD}}}}\)

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Chuyên Lê Quý Đôn - Điện Biên - 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M\) là trung điểm cạnh bên \(SC\). Gọi \(\left( P \right)\) là mặt phẳng chứa \(AM\) và song song với \(BD\), mặt phẳng \(\left( P \right)\) cắt \(SB,SD\) lần lượt tại \(B'\) và \(D'\). Tính tỷ số \(\frac{{{V_{S.AB'MD'}}}}{{{V_{S.ABCD}}}}\) A. … [Đọc thêm...] về

(Chuyên Lê Quý Đôn – Điện Biên – 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M\) là trung điểm cạnh bên \(SC\). Gọi \(\left( P \right)\) là mặt phẳng chứa \(AM\) và song song với \(BD\), mặt phẳng \(\left( P \right)\) cắt \(SB,SD\) lần lượt tại \(B’\) và \(D’\). Tính tỷ số \(\frac{{{V_{S.AB’MD’}}}}{{{V_{S.ABCD}}}}\)

Cho hình lăng trụ tam giác đều\(ABC.A’B’C’\) có cạnh đáy bằng \(1\), cạnh bên bằng \(3\). Gọi \(I\) là điểm trên cạnh \(BB’\) sao cho \(BI = \frac{1}{3}BB’\), điểm \(M\)di động trên cạnh AA’. Biết diện tích của tam giác \(MIC’\) nhỏ nhất khi tỷ số \(\frac{{AM}}{{AA’}} = \frac{a}{b}\,\left( {a \in \mathbb{N};b \in \mathbb{N}*,\,\left( {a,b} \right) = 1} \right)\). \(P = a + b\)là

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:

Câu hỏi: Cho hình lăng trụ tam giác đều\(ABC.A'B'C'\) có cạnh đáy bằng \(1\), cạnh bên bằng \(3\). Gọi \(I\) là điểm trên cạnh \(BB'\) sao cho \(BI = \frac{1}{3}BB'\), điểm \(M\)di động trên cạnh AA'. Biết diện tích của tam giác \(MIC'\) nhỏ nhất khi tỷ số \(\frac{{AM}}{{AA'}} = \frac{a}{b}\,\left( {a \in \mathbb{N};b \in \mathbb{N}*,\,\left( {a,b} \right) = 1} \right)\). … [Đọc thêm...] về

Cho hình lăng trụ tam giác đều\(ABC.A’B’C’\) có cạnh đáy bằng \(1\), cạnh bên bằng \(3\). Gọi \(I\) là điểm trên cạnh \(BB’\) sao cho \(BI = \frac{1}{3}BB’\), điểm \(M\)di động trên cạnh AA’. Biết diện tích của tam giác \(MIC’\) nhỏ nhất khi tỷ số \(\frac{{AM}}{{AA’}} = \frac{a}{b}\,\left( {a \in \mathbb{N};b \in \mathbb{N}*,\,\left( {a,b} \right) = 1} \right)\). \(P = a + b\)là

Cho bát diện đều, tính tỷ số giữa thể tích khối cầu nội tiếp và thể tích khối cầu ngoại tiếp hình bát diện đều đó.

Ngày Thuộc chủ đề:Trắc nghiệm Mặt Cầu Tag với:

Câu hỏi: Cho bát diện đều, tính tỷ số giữa thể tích khối cầu nội tiếp và thể tích khối cầu ngoại tiếp hình bát diện đều đó. A. \(\frac{1}{2}\) B. \(\frac{1}{2\sqrt{2}}\) C. \(\frac{1}{\sqrt{3}}\) D. \(\frac{1}{3\sqrt{3}}\) Lời Giải: Đây là các bài toán Mặt cầu trong phần Hình học 12 - PHẦN MẶT TRÒN XOAY . Gọi cạnh bát diện đều là \(a;\) bát diện đều có các mặt … [Đọc thêm...] vềCho bát diện đều, tính tỷ số giữa thể tích khối cầu nội tiếp và thể tích khối cầu ngoại tiếp hình bát diện đều đó.

Một que kem ốc quế gồm hai phần: phần kem đóng băng có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình nón có bán kính đường tròn đáy bằng bán kính hình cầu. Biết rằng khi kem tan chảy hết thì sẽ làm đầy ốc quế và thể tích phần kem sau khi tan chảy bằng 75% thể tích phần kem đóng băng. Tỷ số giữa chiều cao và bán kính đường tròn đáy của hình nón bằng:

Ngày Thuộc chủ đề:Trắc nghiệm Mặt Cầu Tag với:

Câu hỏi: Một que kem ốc quế gồm hai phần: phần kem đóng băng có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình nón có bán kính đường tròn đáy bằng bán kính hình cầu. Biết rằng khi kem tan chảy hết thì sẽ làm đầy ốc quế và thể tích phần kem sau khi tan chảy bằng 75% thể tích phần kem đóng băng. Tỷ số giữa chiều cao và bán kính đường tròn đáy của hình nón bằng: A. … [Đọc thêm...] vềMột que kem ốc quế gồm hai phần: phần kem đóng băng có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình nón có bán kính đường tròn đáy bằng bán kính hình cầu. Biết rằng khi kem tan chảy hết thì sẽ làm đầy ốc quế và thể tích phần kem sau khi tan chảy bằng 75% thể tích phần kem đóng băng. Tỷ số giữa chiều cao và bán kính đường tròn đáy của hình nón bằng:

Xét một hình trụ nội tiếp tronh hình nón như hình bên dưới , trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ ; AC, BD cắt nhau tại điểm \(M\in SO.\) Biết rằng tỉ số thể tích của hình trụ và hình nón là \(\frac{4}{9}.\) Tính tỷ số \(\frac{SM}{SO}.\)

Ngày Thuộc chủ đề:Trắc nghiệm Mặt Nón Tag với:

Câu hỏi: Xét một hình trụ nội tiếp tronh hình nón như hình bên dưới , trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ ; AC, BD cắt nhau tại điểm \(M\in SO.\) Biết rằng tỉ số thể tích của hình trụ và hình nón là \(\frac{4}{9}.\) Tính tỷ số \(\frac{SM}{SO}.\) A. \(\frac{7}{9}\) B. … [Đọc thêm...] vềXét một hình trụ nội tiếp tronh hình nón như hình bên dưới , trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ ; AC, BD cắt nhau tại điểm \(M\in SO.\) Biết rằng tỉ số thể tích của hình trụ và hình nón là \(\frac{4}{9}.\) Tính tỷ số \(\frac{SM}{SO}.\)

Cho hàm số\(y = f(x) = a{x^4} + b{x^2} + c\) có đồ thị \(\left( C \right),\) Biết\(f( – 1) = 0\). Tiếp tuyến \(d\) tại điểm có hoành độ \(x =  – 1\) của \(\left( C \right)\) cắt \(\left( C \right)\) tại 2 điểm có hoành độ lần lượt là 0 và 2, Gọi \({S_1};{S_2}\) là diện tích hình phẳng. Tính tỷ số \(\frac{{{S_1}}}{{{S_2}}}\) 

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:, ,

DẠNG TOÁN 48 : ỨNG DỤNG TÍCH PHÂN (TÍNH DIỆN TÍCH HÌNH PHẲNG, TỈ SỐ DIỆN TÍCH)   Theo đề tham khảo Toán 2021 ĐỀ BÀI: Cho hàm số\(y = f(x) = a{x^4} + b{x^2} + c\) có đồ thị \(\left( C \right),\) Biết\(f( - 1) = 0\). Tiếp tuyến \(d\) tại điểm có hoành độ \(x =  - 1\) của \(\left( C \right)\) cắt \(\left( C \right)\) tại 2 điểm có hoành độ lần lượt là 0 … [Đọc thêm...] vềCho hàm số\(y = f(x) = a{x^4} + b{x^2} + c\) có đồ thị \(\left( C \right),\) Biết\(f( – 1) = 0\). Tiếp tuyến \(d\) tại điểm có hoành độ \(x =  – 1\) của \(\left( C \right)\) cắt \(\left( C \right)\) tại 2 điểm có hoành độ lần lượt là 0 và 2, Gọi \({S_1};{S_2}\) là diện tích hình phẳng. Tính tỷ số \(\frac{{{S_1}}}{{{S_2}}}\)