DẠNG TOÁN 48 : ỨNG DỤNG TÍCH PHÂN (TÍNH DIỆN TÍCH HÌNH PHẲNG, TỈ SỐ DIỆN TÍCH) Theo đề tham khảo Toán 2021 ĐỀ BÀI: Cho hàm số \(y = \frac{1}{2}{x^3} + b{x^2} + 3\) có đồ thì \(\left( C \right)\). Đường thẳng \(y = 1\) là tiếp tuyến tại điểm cực tiểu có hoành độ \({x_2}\) của đồ thị \(\left( C \right)\) đồng thời cắt đồ thị \(\left( C \right)\) tại điểm … [Đọc thêm...] vềCho hàm số \(y = \frac{1}{2}{x^3} + b{x^2} + 3\) có đồ thì \(\left( C \right)\). Đường thẳng \(y = 1\) là tiếp tuyến tại điểm cực tiểu có hoành độ \({x_2}\) của đồ thị \(\left( C \right)\) đồng thời cắt đồ thị \(\left( C \right)\) tại điểm có hoành độ \({x_1}\). Tính tỷ số diện tích \(\frac{{{S_1}}}{{{S_2}}}\)với \({S_1},\,{S_2}\) được thể hiện trong hình vẽ.
Kết quả tìm kiếm cho: ty so
Cho hàm số \(y = \left| {f\left( x \right)} \right|\) có đồ thị là đường cong trong hình vẽ, với \(f\left( x \right)\) là hàm số bậc ba. Biết hàm số \(f\left( x \right)\) đạt cực trị tại điểm \({x_1};\,{x_2}\) thỏa mãn \({x_2} = {x_1} + 2\) và \(f\left( {{x_1}} \right) + f\left( {{x_2}} \right) = 0\). Gọi \({S_1},\,{S_2}\) là diện tích của hai hình phẳng được tô trong hình vẽ dưới đây. Tỷ số \(\frac{{{S_1}}}{{{S_2}}}\)bằng
DẠNG TOÁN 48 : ỨNG DỤNG TÍCH PHÂN (TÍNH DIỆN TÍCH HÌNH PHẲNG, TỈ SỐ DIỆN TÍCH) Theo đề tham khảo Toán 2021 ĐỀ BÀI: Cho hàm số \(y = \left| {f\left( x \right)} \right|\) có đồ thị là đường cong trong hình vẽ, với \(f\left( x \right)\) là hàm số bậc ba. Biết hàm số \(f\left( x \right)\) đạt cực trị tại điểm \({x_1};\,{x_2}\) thỏa mãn \({x_2} = {x_1} + 2\) … [Đọc thêm...] vềCho hàm số \(y = \left| {f\left( x \right)} \right|\) có đồ thị là đường cong trong hình vẽ, với \(f\left( x \right)\) là hàm số bậc ba. Biết hàm số \(f\left( x \right)\) đạt cực trị tại điểm \({x_1};\,{x_2}\) thỏa mãn \({x_2} = {x_1} + 2\) và \(f\left( {{x_1}} \right) + f\left( {{x_2}} \right) = 0\). Gọi \({S_1},\,{S_2}\) là diện tích của hai hình phẳng được tô trong hình vẽ dưới đây. Tỷ số \(\frac{{{S_1}}}{{{S_2}}}\)bằng
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong như hình vẽ bên. Biết hàm số đạt cực trị tại các điểm \({x_1},\,{x_2},\,{x_3}\) theo thứ tự lập thành cấp số cộng có công sai bằng 1 và \(f\left( {{x_1}} \right) = f\left( {{x_3}} \right)\), gọi \({S_1},\,{S_2}\) là diện tích hai hình phẳng được gạch trong hình bên. Tính tỷ số \(\frac{{{S_1}}}{{{S_2}}}.\)
DẠNG TOÁN 48 : ỨNG DỤNG TÍCH PHÂN (TÍNH DIỆN TÍCH HÌNH PHẲNG, TỈ SỐ DIỆN TÍCH) Theo đề tham khảo Toán 2021 ĐỀ BÀI: Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong như hình vẽ bên. Biết hàm số đạt cực trị tại các điểm \({x_1},\,{x_2},\,{x_3}\) theo thứ tự lập thành cấp số cộng có công sai bằng 1 và \(f\left( {{x_1}} \right) = f\left( … [Đọc thêm...] vềCho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong như hình vẽ bên. Biết hàm số đạt cực trị tại các điểm \({x_1},\,{x_2},\,{x_3}\) theo thứ tự lập thành cấp số cộng có công sai bằng 1 và \(f\left( {{x_1}} \right) = f\left( {{x_3}} \right)\), gọi \({S_1},\,{S_2}\) là diện tích hai hình phẳng được gạch trong hình bên. Tính tỷ số \(\frac{{{S_1}}}{{{S_2}}}.\)
Cho hàm số \(y = f(x) = {x^3} – 3x + 1\)và điểm \(M({x_0};{y_0})\)thuộc đồ thị của hàm số \(y = f(x)\) như hình vẽ. Đường thẳng \(OM\) cắt đồ thị tại 3 điểm có hoành độ \({x_0},{x_1},{x_2}\) thỏa mãn \({x_0} < – 1 < 0 < {x_1} < {x_2}\) và \({x_1}^2 + {x_0}{x_1} – {x_1}{x_2} = – 1\). Tỷ số diện tích \(\frac{{{S_1}}}{{{S_2}}}\) nằm trong khoảng nào dưới đây
DẠNG TOÁN 48 : ỨNG DỤNG TÍCH PHÂN (TÍNH DIỆN TÍCH HÌNH PHẲNG, TỈ SỐ DIỆN TÍCH) Theo đề tham khảo Toán 2021 ĐỀ BÀI: Cho hàm số \(y = f(x) = {x^3} - 3x + 1\)và điểm \(M({x_0};{y_0})\)thuộc đồ thị của hàm số \(y = f(x)\) như hình vẽ. Đường thẳng \(OM\) cắt đồ thị tại 3 điểm có hoành độ \({x_0},{x_1},{x_2}\) thỏa mãn \({x_0} < - 1 < 0 < {x_1} … [Đọc thêm...] vềCho hàm số \(y = f(x) = {x^3} – 3x + 1\)và điểm \(M({x_0};{y_0})\)thuộc đồ thị của hàm số \(y = f(x)\) như hình vẽ. Đường thẳng \(OM\) cắt đồ thị tại 3 điểm có hoành độ \({x_0},{x_1},{x_2}\) thỏa mãn \({x_0} < – 1 < 0 < {x_1} < {x_2}\) và \({x_1}^2 + {x_0}{x_1} – {x_1}{x_2} = – 1\). Tỷ số diện tích \(\frac{{{S_1}}}{{{S_2}}}\) nằm trong khoảng nào dưới đây
Phát triển câu 49 đề tốt nghiệp THPT 2020 – TỶ SỐ Thể tích khối đa diện
Phát triển câu 49 đề tốt nghiệp THPT 2020 – TỶ SỐ Thể tích khối đa diện ============== ================= =========== LINK NHÓM GEO ✦ Dạng toán 49. Thể tích khối đa diện (cắt bởi mặt phẳng). → https://bit.ly/2VOiJlQ =============== … [Đọc thêm...] vềPhát triển câu 49 đề tốt nghiệp THPT 2020 – TỶ SỐ Thể tích khối đa diện
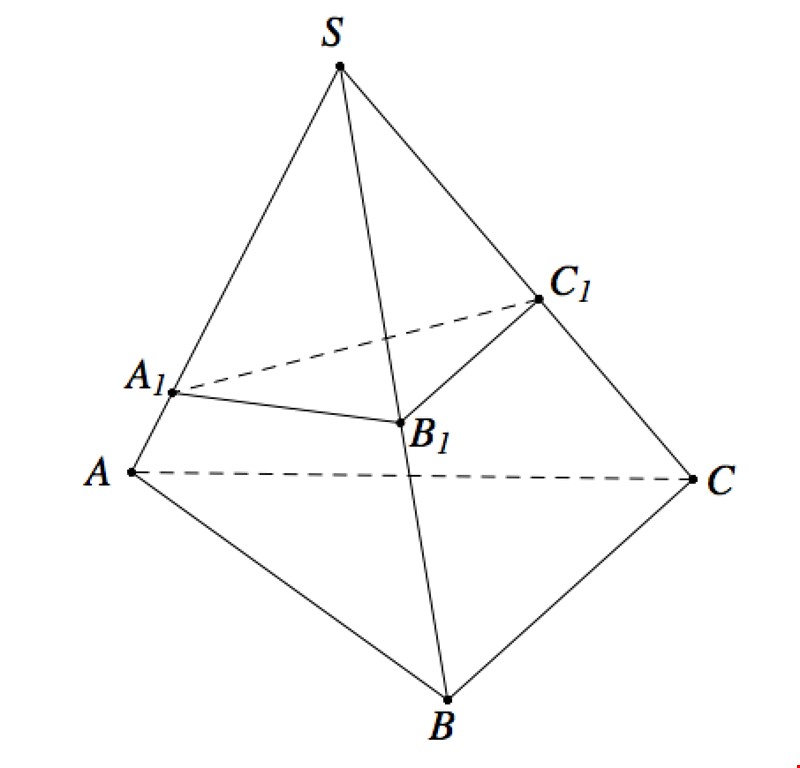
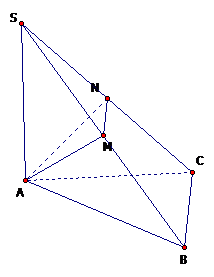
Đề: Cho hình chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho \(SA' = \frac{1}{2}SA\); \(SB' = \frac{1}{2}SB;SC' = \frac{1}{2}SC\). Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và khối đa diện ABCA’B’C’. Tính tỷ số \(\frac{{V'}}{V}\).
Câu hỏi: Cho hình chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho \(SA' = \frac{1}{2}SA\); \(SB' = \frac{1}{2}SB;SC' = \frac{1}{2}SC\). Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và khối đa diện ABCA’B’C’. Tính tỷ số \(\frac{{V'}}{V}\). A. \(\frac{7}{8}\) B. \(\frac{7}{12}\) C. … [Đọc thêm...] vềĐề: Cho hình chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho \(SA' = \frac{1}{2}SA\); \(SB' = \frac{1}{2}SB;SC' = \frac{1}{2}SC\). Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và khối đa diện ABCA’B’C’. Tính tỷ số \(\frac{{V'}}{V}\).
Các công thức tính nhanh Tỷ số thể tích khối đa diện
Tổng hợp tất cả các công thức tính nhanh Tỷ số thể tích khối đa diện ----------------- Công thức 1: Hai khối chóp chung đỉnh và chung mặt phẳng đáy $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{{{S}_{1}}}{{{S}_{2}}}.$ Câu 1. Cho khối chóp $S.ABC$ có thể tích $V.$ Gọi $M,N,P$ lần lượt là trung điểm các cạnh $BC,CA,AB$ và ${V}'$ là thể tích khối chóp $S.MNP.$ Tính tỉ số … [Đọc thêm...] vềCác công thức tính nhanh Tỷ số thể tích khối đa diện
Tỷ số thể tích khối đa diện
Tỷ số thể tích khối đa diện Công thức tỉ số thể tích của khối chóp tam giác: Trên các đường thẳng SA, SB, SC của hình chóp S.ABC ta lấy lần lượt các điểm A', B', C'. Ta có: $\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}.$ Ví dụ 1: Cho hình chóp S.ABC có tam giác ABC đều cạnh 2a, cạnh bên SA vuông góc với … [Đọc thêm...] vềTỷ số thể tích khối đa diện
Hàm số nào dưới đây có bảng biến thiên như sau?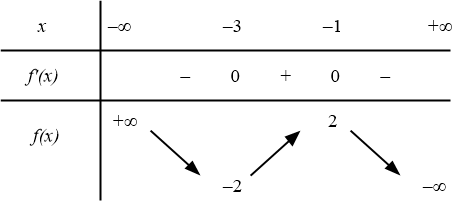

Bài toán gốc Hàm số nào dưới đây có bảng biến thiên như sau?A. $y=x^3-6x^2-9x+2$.B. $y=x^3+6x^2+9x+2$.C. $y=-x^3+6x^2+9x-2$.D. $y=-x^3-6x^2-9x-2$. Phân tích và Phương pháp giải Dạng toán: Nhận dạng hàm số bậc ba $y = ax^3 + bx^2 + cx + d$ thông qua bảng biến thiên (BBT). Phương pháp giải: 1. Quan sát giới hạn (khi $x \to \pm\infty$) để xác định … [Đọc thêm...] vềHàm số nào dưới đây có bảng biến thiên như sau?

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây: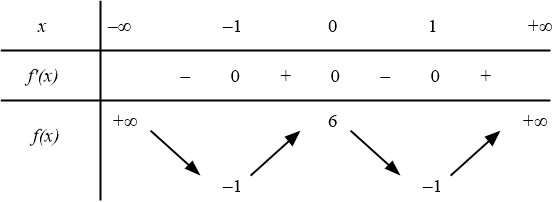

Bài toán gốc Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:Có bao nhiêu giá trị nguyên $m$ để phương trình $f(x)-5=m$ có 3 nghiệm hoặc 4 nghiệm?A. $6$.B. $7$.C. $10$.D. $9$. Phân tích và Phương pháp giải Dạng toán này yêu cầu biện luận số nghiệm của phương trình chứa tham số dựa trên đồ thị/Bảng biến thiên (BBT) của hàm số $y=f(x)$. … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây: