Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
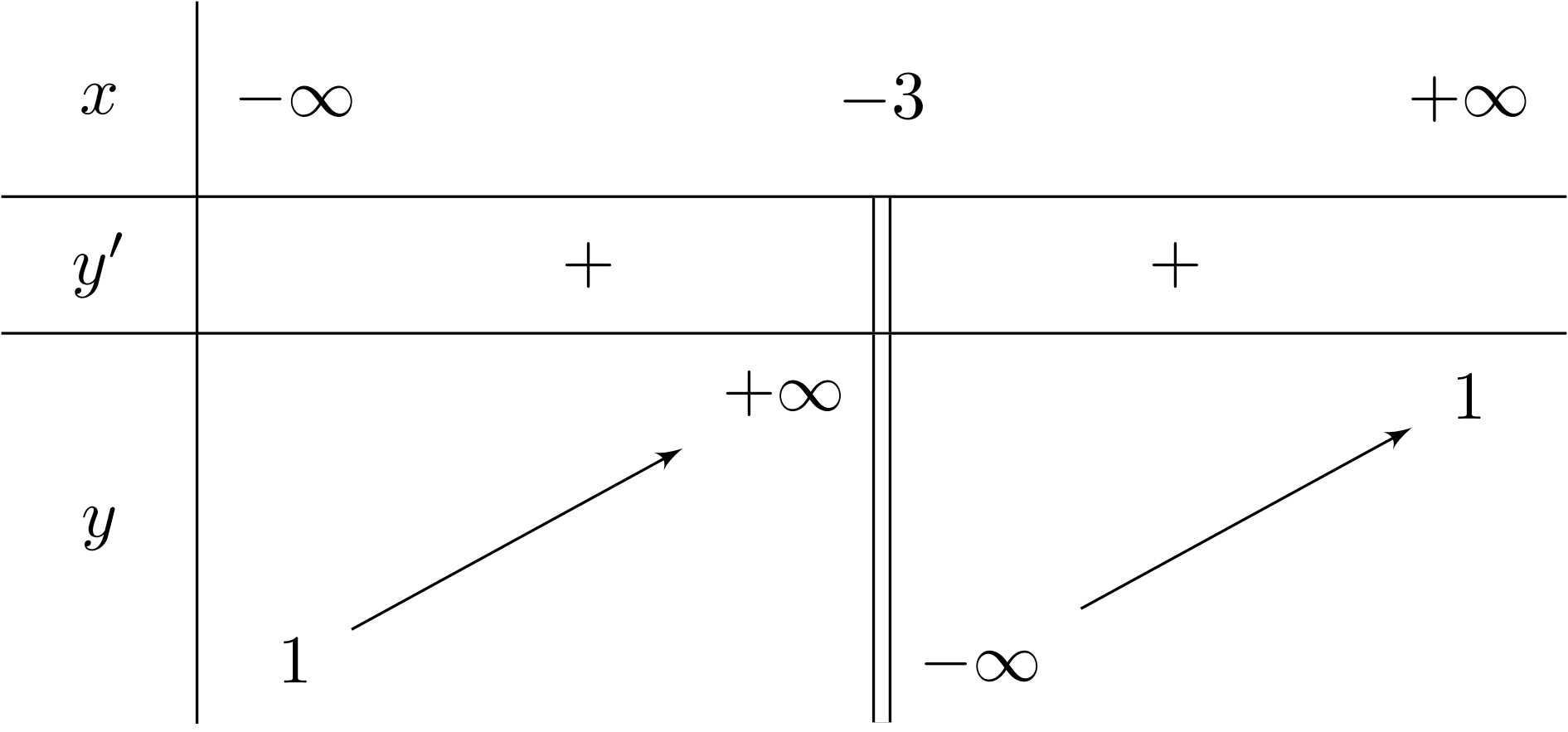
Bài toán gốc Cho hàm số $y = \dfrac{-x+5}{-x-3}$ có bảng biến thiên bên dưới. Đồ thị hàm số có tiệm cận ngang làA. $x = 1$.B. $x = 1$.C. $y = 1$.D. $y = -3$.Lời giải: Dựa vào bảng biến thiên ta được tiệm cận ngang là $x = 1$. Phân tích và Phương pháp giải Đây là dạng toán tìm tiệm cận ngang (TCN) của hàm số hữu tỉ $y = \dfrac{ax+b}{cx+d}$. … [Đọc thêm...] vềCho hàm số $y = \dfrac{-x+5}{-x-3}$ có bảng biến thiên bên dưới. Đồ thị hàm số có tiệm cận ngang là
Một công ty đánh giá rằng sẽ bán được $N$ lô hàng nếu chi hết số tiền là $x$ (triệu đồng) vào việc quảng cáo. Biết rằng $N$ và $x$ liên hệ với nhau bằng biểu thức $N\left( x \right)=-{{x}^{2}}+30x+6,0\le x\le 30$. Hãy tìm số lô hàng lớn nhất mà công ti có thể bán sau đợt quảng cáo?Đáp án: 15Lời giải: Ta có $N\left( x \right)=-{{x}^{2}}+30x+6\Rightarrow {N}'\left( x … [Đọc thêm...] vềMột công ty đánh giá rằng sẽ bán được $N$ lô hàng nếu chi hết số tiền là $x$ (triệu đồng) vào việc quảng cáo
Giả sử một công ty du lịch bán tour với giá là $x$ (triệu đồng)/khách thì doanh thu sẽ được biểu diễn qua hàm số $f(x)=-200{{x}^{2}}+550x$. Công ty phải bán giá tour cho một khách là bao nhiêu để doanh thu từ tua xuyên Việt là lớn nhất (làm tròn tới hàng phần trăm).Đáp án: 1,38Lời giải: Doanh thu là $f(x)=-200{{x}^{2}}+550x$. Ta có ${f}'\left( x \right)=-400x+550$. ${f}'\left( … [Đọc thêm...] vềGiả sử một công ty du lịch bán tour với giá là $x$ (triệu đồng)/khách thì doanh thu sẽ được biểu diễn qua hàm số $f(x)=-200{{x}^{2}}+550x$
Nhằm tăng tính cạnh tranh trên thị trường vào dịp Tết Nguyên Đán, công ty nước giải khát K dự định bổ sung một số sản phẩm mới trong đó có mẫu lon nước giải khát dung tích $500ml$ (mililit) dạng hình trụ. Để giảm chi phí logistic các nhà thiết kế cần thiết kế mẫu lon nước này có bán kính đường tròn đáy bằng bao nhiêu centimet để tiết kiệm vật liệu nhất? (Kết quả làm tròn đến … [Đọc thêm...] vềNhằm tăng tính cạnh tranh trên thị trường vào dịp Tết Nguyên Đán, công ty nước giải khát K dự định bổ sung một số sản phẩm mới trong đó có mẫu lon nước giải khát dung tích $500ml$ (mililit) dạng hình trụ
Hàm số $y={{\log }_{3}}\left( {{x}^{2}}-2x \right)$ nghịch biến trên khoảng $\left( -\infty ;a \right)$ có độ dài lớn nhất. Khi đó a bằng?Đáp án: 0Lời giải: Hàm số $y={{\log }_{3}}\left( {{x}^{2}}-2x \right)$ có tập xác định $D=\left( -\infty ;0 \right)\cup \left( 2;+\infty \right)$. Ta có ${y}'=\dfrac{2x-2}{\left( {{x}^{2}}-2x \right)\ln 3}$. Khi đó ${y}'=0$ $\Leftrightarrow$ … [Đọc thêm...] vềHàm số $y={{\log }_{3}}\left( {{x}^{2}}-2x \right)$ nghịch biến trên khoảng $\left( -\infty ;a \right)$ có độ dài lớn nhất
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau: a) Hàm số $y=f\left( x \right)$ nghịch biến trên $\left( 0;1 \right)$.b) Hàm số $y=f\left( x \right)$ đồng biến trên $\left( -\infty ;-1 \right)$.c) Hàm số $y=f\left( x \right)$ có 2 điểm cực trị.d) Giá trị lớn nhất của $g\left( x \right)=f\left( x \right)+\sin x$ trên đoạn $\left[ -\dfrac{\pi }{2};-1 \right]$ là … [Đọc thêm...] vềCho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
Cho hàm số $f\left( x \right)=\ln x-2{{x}^{2}}$, $\forall x\in \left( 0;+\infty \right)$.a) Hàm số trên luôn đồng biến trên tập xác định. .b) $f\left( 1 \right)=-2;f\left( {{\text{e}}^{2}} \right)=2-2{{\text{e}}^{4}}.$ .c) Hàm số $y=f\left( x \right)$ có một điểm cực trị. .d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\left[ 1;{{\text{e}}^{2}} \right]$ là … [Đọc thêm...] vềCho hàm số $f\left( x \right)=\ln x-2{{x}^{2}}$, $\forall x\in \left( 0;+\infty \right)$
Xét tính đúng sai của các phát biểu sau:
Bài toán gốc Hàm số $y=f(x)$ có bảng biến trên $[-2;3]$ như hình dưới đây:Xét tính đúng sai của các phát biểu sau:a) Hàm số đồng biến trên $(0;3)$.b) Cực tiểu hàm số trên khoảng $(-2;3)$ bằng $2$.c) Hàm số đạt giá trị lớn nhất trên $[-2;3]$ tại điểm $x=3$.d) Hàm số đạt giá trị lớn nhất trên $[-2;3]$ tại điểm $x=2$.Lời giải: (Sai) Hàm số đồng biến trên $(0;3)$.(Sai) Cực … [Đọc thêm...] vềHàm số $y=f(x)$ có bảng biến trên $[-2;3]$ như hình dưới đây:
Xét tính đúng sai của các phát biểu sau:
a) Hàm số đồng biến trên $(3;+\infty)$
Bài toán gốc Hàm số $y=2x^3-12x^2+18x+4$. Xét tính đúng sai của các phát biểu sau:a) Hàm số đồng biến trên $(3;+\infty)$.b) Hàm số trên khoảng $(0;5)$ đạt cực tiểu tại điểm $x=1$.c) Giá trị lớn nhất của hàm số trên $[0;5]$ bằng $12$.d) Giá trị nhỏ nhất của hàm số trên $[0;5]$ bằng $4$.Lời giải: $y^{\prime}=6x^2-24x+18$$y^{\prime}=0\Leftrightarrow x_1=1,x_2=3$.(Đúng) Hàm … [Đọc thêm...] vềHàm số $y=2x^3-12x^2+18x+4$. Xét tính đúng sai của các phát biểu sau:
a) Hàm số đồng biến trên $(3;+\infty)$
Bài toán gốc Tìm giá trị nhỏ nhất của hàm số $y=x+\dfrac{1}{x}+4$ trên $(0;+\infty)$.A. $6$.B. $9$.C. $4$.D. $3$. Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị nhỏ nhất của hàm số trên một khoảng xác định. Do hàm số có cấu trúc dạng $x + 1/x + C$ với $x > 0$, phương pháp hiệu quả nhất là sử dụng Bất đẳng thức Cô-si (AM-GM): $a+b \ge … [Đọc thêm...] vềTìm giá trị nhỏ nhất của hàm số $y=x+\dfrac{1}{x}+4$ trên $(0;+\infty)$.