Bài toán gốc
Cho hàm số $y = \dfrac{-x+5}{-x-3}$ có bảng biến thiên bên dưới. Đồ thị hàm số có tiệm cận ngang là
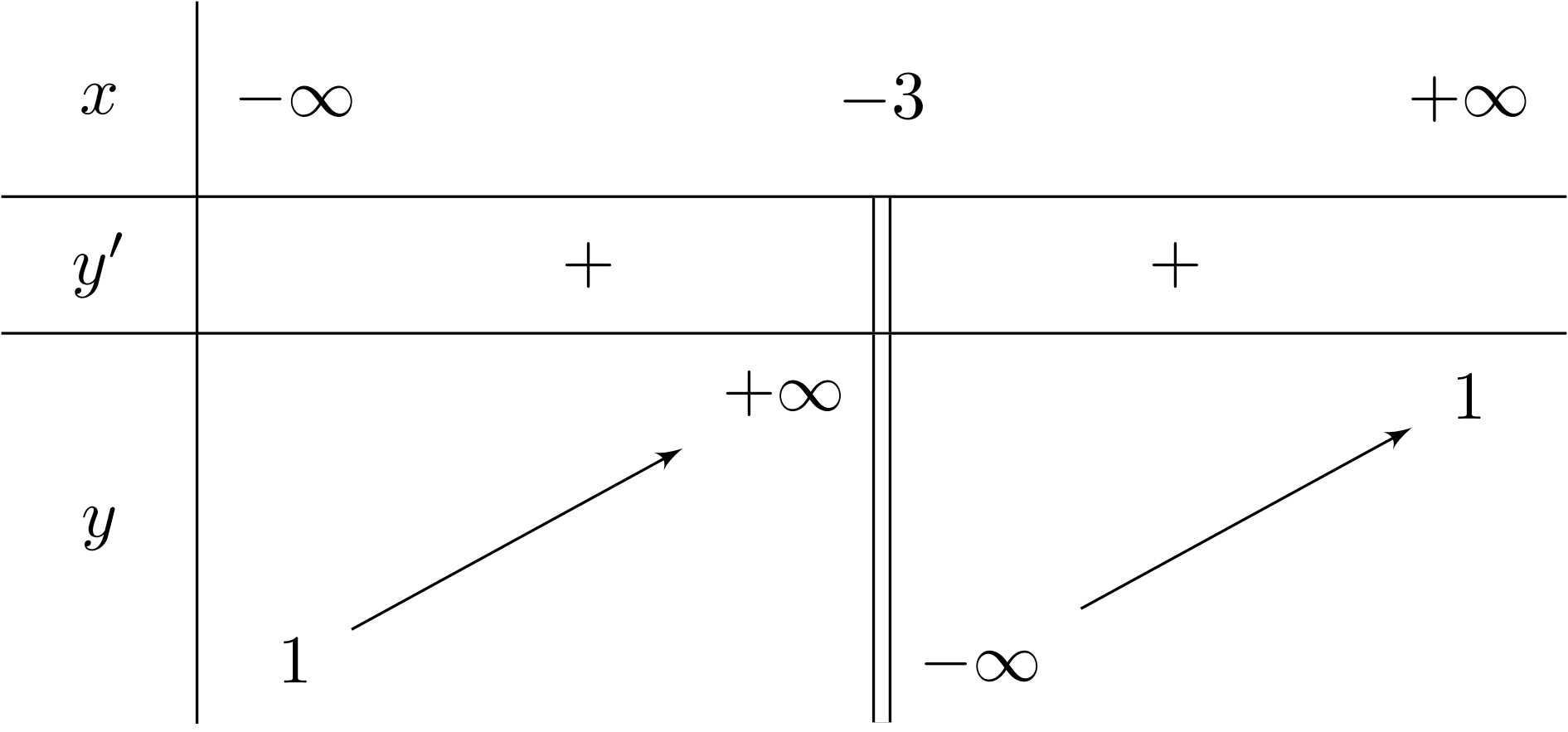
A. $x = 1$.
B. $x = 1$.
C. $y = 1$.
D. $y = -3$.
Lời giải: Dựa vào bảng biến thiên ta được tiệm cận ngang là $x = 1$.
Phân tích và Phương pháp giải
Đây là dạng toán tìm tiệm cận ngang (TCN) của hàm số hữu tỉ $y = \dfrac{ax+b}{cx+d}$. Phương pháp giải là xác định giới hạn của hàm số khi $x$ tiến tới vô cùng. TCN là đường thẳng $y = \dfrac{a}{c}$. Trong bài toán gốc, $y = \dfrac{-1x+5}{-1x-3}$, suy ra TCN là $y = \dfrac{-1}{-1} = 1$.
Bài toán tương tự
Cho hàm số $y = \dfrac{3x-5}{6x+1}$. Đồ thị hàm số có tiệm cận ngang là: A. $y = -1/6$. B. $x = -1/6$. C. $y = 1/2$. D. $y = 3$. Đáp án đúng: C. Lời giải: Tiệm cận ngang của hàm số $y = \dfrac{ax+b}{cx+d}$ là $y = \dfrac{a}{c}$. Với $a=3$ và $c=6$, ta có TCN là $y = \dfrac{3}{6} = \dfrac{1}{2}$.
