Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây đồ thị hàm số sẽ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

Bài toán gốc

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây đồ thị hàm số sẽ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

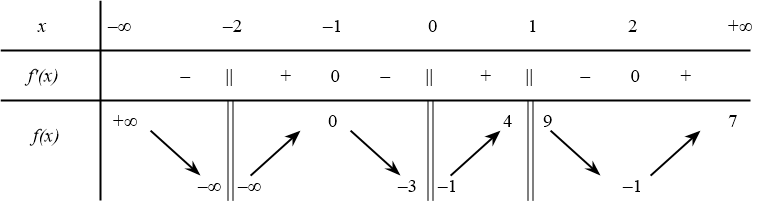
A. 2.

B. 4.

C. 3.

D. 5.

Lời giải: Có thay đổi kết quả

Phân tích và Phương pháp giải

Dạng bài toán là xác định số lượng tiệm cận đứng (TCĐ) và tiệm cận ngang (TCN) của đồ thị hàm số dựa vào bảng biến thiên đã cho. Phương pháp là: Tiệm cận ngang được xác định bằng cách xét giới hạn của hàm số khi x tiến ra vô cùng (lim(y) = hằng số khi x -> +/- vô cùng). Tiệm cận đứng được xác định bằng cách xét giới hạn của hàm số tại các điểm không xác định của hàm số mà tại đó y tiến về vô cùng (lim(y) = +/- vô cùng khi x -> x0).

Bài toán tương tự

Cho hàm số $y=g(x)$ có bảng biến thiên (BBT) như sau: Tập xác định của hàm số là $D=(-\infty; -1) \cup (-1; 2) \cup (2; +\infty)$. Trong BBT, ta có: (1) Khi $x \to -\infty$, $y \to 5$. (2) Khi $x \to -1^-$, $y \to +\infty$. (3) Khi $x \to -1^+$, $y \to -\infty$. (4) Khi $x \to 2^-$, $y \to 1$. (5) Khi $x \to 2^+$, $y \to -\infty$. (6) Khi $x \to +\infty$, $y \to 5$. Hỏi đồ thị hàm số $y=g(x)$ có tổng cộng bao nhiêu đường tiệm cận? A. 3. B. 4. C. 5. D. 2. Đáp án đúng: A. Giải thích: Tiệm cận ngang (TCN): $\lim_{x \to -\infty} y = 5$ và $\lim_{x \to +\infty} y = 5$. Vì hai giới hạn này bằng nhau, đồ thị chỉ có 1 đường TCN là $y=5$. Tiệm cận đứng (TCĐ): Tại $x=-1$, $\lim_{x \to -1^-} y = +\infty$ và $\lim_{x \to -1^+} y = -\infty$. Vậy $x=-1$ là 1 đường TCĐ. Tại $x=2$, $\lim_{x \to 2^+} y = -\infty$. Vậy $x=2$ là 1 đường TCĐ. Tổng số đường tiệm cận: $1 ext{ (TCN)} + 2 ext{ (TCĐ)} = 3$ đường.