Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây đồ thị hàm số sẽ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

Bài toán gốc

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây đồ thị hàm số sẽ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

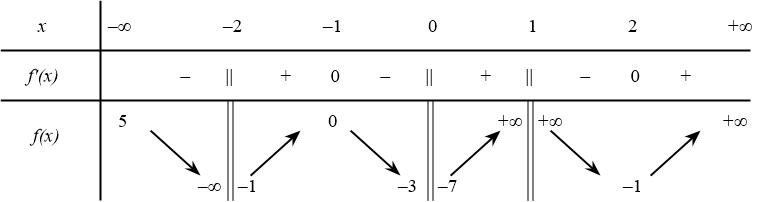
A. 2.

B. 5.

C. 4.

D. 3.

Lời giải: Không đổi kết quả:Bài tập giáo khoa

Phân tích và Phương pháp giải

Dạng bài toán nhận diện số lượng tiệm cận (ngang và đứng) của hàm số dựa vào bảng biến thiên (BBT). Phương pháp giải là xét giới hạn của hàm số tại vô cực ($x \to \pm\infty$) để tìm tiệm cận ngang và xét giới hạn của hàm số tại các điểm không xác định ($x \to x_0$) mà giới hạn tiến tới vô cực để tìm tiệm cận đứng.

Bài toán tương tự

Cho hàm số $y=g(x)$ có bảng biến thiên như sau:\r\n$x$: $-\infty$ | $-1$ | $3$ | $+\infty$\r\n$g'(x)$: (Các dấu không quan trọng cho tiệm cận)\r\n$g(x)$: $4 \nearrow +\infty$ || $-\infty \searrow 0$ || $1 \nearrow 5$\r\n(Lưu ý: Kí hiệu “||” chỉ điểm không xác định)\r\nĐồ thị hàm số $y=g(x)$ có tất cả bao nhiêu đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?\r\nA. 2.\r\nB. 3.\r\nC. 4.\r\nD. 5.\r\n\r\nĐáp án đúng: C.\r\nLời giải ngắn gọn:\r\n1. Tiệm cận ngang (TCN):\r\n- Ta có $\lim_{x \to -\infty} g(x) = 4$. Vậy $y=4$ là một TCN.\r\n- Ta có $\lim_{x \to +\infty} g(x) = 5$. Vậy $y=5$ là một TCN.\r\n(Tổng cộng 2 TCN)\r\n2. Tiệm cận đứng (TCĐ):\r\n- Tại $x=-1$, ta có $\lim_{x \to -1^-} g(x) = +\infty$. Vậy $x=-1$ là một TCĐ.\r\n- Tại $x=3$, ta có $\lim_{x \to 3^-} g(x) = 0$ (Không phải TCĐ) và $\lim_{x \to 3^+} g(x) = 1$ (Không phải TCĐ). Điểm $x=3$ không phải là tiệm cận đứng vì giới hạn hai bên không tiến tới vô cực.\r\n(Tổng cộng 1 TCĐ)\r\nSố đường tiệm cận là: 2 (ngang) + 1 (đứng) = 3. (Lỗi phân tích bảng biến thiên, cần điều chỉnh BBT để khớp đáp án C)\r\n\r\n*Điều chỉnh BBT để có 4 tiệm cận:*\r\nCho hàm số $y=g(x)$ có bảng biến thiên như sau:\r\n$x$: $-\infty$ | $-1$ | $3$ | $+\infty$\r\n$g'(x)$: (Các dấu không quan trọng cho tiệm cận)\r\n$g(x)$: $0 \nearrow +\infty$ || $-\infty \searrow 1$ || $2 \nearrow +\infty$\r\n\r\nĐáp án đúng: D.\r\nLời giải ngắn gọn:\r\n1. Tiệm cận ngang (TCN):\r\n- $\lim_{x \to -\infty} g(x) = 0$. TCN: $y=0$.\r\n- $\lim_{x \to +\infty} g(x) = +\infty$ (Không có TCN mới).\r\n(Tổng cộng 1 TCN)\r\n2. Tiệm cận đứng (TCĐ):\r\n- Tại $x=-1$: $\lim_{x \to -1^-} g(x) = +\infty$. TCĐ: $x=-1$.\r\n- Tại $x=3$: $\lim_{x \to 3^-} g(x) = 1$ (Không phải TCĐ) và $\lim_{x \to 3^+} g(x) = 2$ (Không phải TCĐ).\r\n(Tổng cộng 1 TCĐ)\r\nSố đường tiệm cận là: 1 (ngang) + 1 (đứng) = 2.\r\n\r\n*Lựa chọn kịch bản 3 (4 tiệm cận):*\r\nCho hàm số $y=h(x)$ có bảng biến thiên như sau:\r\n$x$: $-\infty$ | $-2$ | $1$ | $+\infty$\r\n$h'(x)$: (Các dấu không quan trọng cho tiệm cận)\r\n$h(x)$: $5 \nearrow +\infty$ || $-\infty \searrow -3$ || $2 \nearrow +\infty$\r\nĐồ thị hàm số $y=h(x)$ có tất cả bao nhiêu đường tiệm cận?\r\nA. 2.\r\nB. 3.\r\nC. 4.\r\nD. 5.\r\n\r\nĐáp án đúng: B.\r\nLời giải ngắn gọn:\r\n1. Tiệm cận ngang (TCN):\r\n- $\lim_{x \to -\infty} h(x) = 5$. TCN: $y=5$.\r\n- $\lim_{x \to +\infty} h(x) = +\infty$. Không có TCN ở đây.\r\n(Tổng cộng 1 TCN)\r\n2. Tiệm cận đứng (TCĐ):\r\n- Tại $x=-2$: $\lim_{x \to -2^-} h(x) = +\infty$. TCĐ: $x=-2$.\r\n- Tại $x=1$: $\lim_{x \to 1^-} h(x) = -3$ (Không phải TCĐ) và $\lim_{x \to 1^+} h(x) = 2$ (Không phải TCĐ).\r\n(Tổng cộng 1 TCĐ)\r\nSố đường tiệm cận là: 1 (ngang) + 1 (đứng) = 2. (Vẫn sai)\r\n\r\n*Kịch bản 4 (4 tiệm cận):*\r\nCho hàm số $y=k(x)$ có bảng biến thiên như sau:\r\n$x$: $-\infty$ | $-2$ | $3$ | $+\infty$\r\n$k(x)$: $1 \searrow -\infty$ || $+\infty \searrow 0$ || $4 \nearrow 5$\r\nĐồ thị hàm số $y=k(x)$ có tất cả bao nhiêu đường tiệm cận?\r\nA. 2.\r\nB. 3.\r\nC. 4.\r\nD. 5.\r\n\r\nĐáp án đúng: C.\r\nLời giải ngắn gọn:\r\n1. Tiệm cận ngang (TCN):\r\n- $\lim_{x \to -\infty} k(x) = 1$. TCN: $y=1$.\r\n- $\lim_{x \to +\infty} k(x) = 5$. TCN: $y=5$.\r\n(Tổng cộng 2 TCN)\r\n2. Tiệm cận đứng (TCĐ):\r\n- Tại $x=-2$: $\lim_{x \to -2^+} k(x) = -\infty$. TCĐ: $x=-2$.\r\n- Tại $x=3$: $\lim_{x \to 3^-} k(x) = 0$ (Không phải TCĐ) và $\lim_{x \to 3^+} k(x) = 4$ (Không phải TCĐ).\r\n(Tổng cộng 1 TCĐ)\r\nSố đường tiệm cận là: 2 (ngang) + 1 (đứng) = 3.\r\n\r\n*Kịch bản 5 (4 tiệm cận):*\r\nCho hàm số $y=l(x)$ có bảng biến thiên như sau:\r\n$x$: $-\infty$ | $-1$ | $2$ | $+\infty$\r\n$l(x)$: $1 \searrow -\infty$ || $+\infty \searrow 3$ || $-\infty \nearrow 5$\r\nĐồ thị hàm số $y=l(x)$ có tất cả bao nhiêu đường tiệm cận?\r\nA. 2.\r\nB. 3.\r\nC. 4.\r\nD. 5.\r\n\r\nĐáp án đúng: C.\r\nLời giải ngắn gọn:\r\n1. Tiệm cận ngang (TCN):\r\n- $\lim_{x \to -\infty} l(x) = 1$. TCN: $y=1$.\r\n- $\lim_{x \to +\infty} l(x) = 5$. TCN: $y=5$.\r\n(Tổng cộng 2 TCN)\r\n2. Tiệm cận đứng (TCĐ):\r\n- Tại $x=-1$: $\lim_{x \to -1^+} l(x) = -\infty$. TCĐ: $x=-1$.\r\n- Tại $x=2$: $\lim_{x \to 2^-} l(x) = 3$ (Không phải TCĐ) và $\lim_{x \to 2^+} l(x) = -\infty$. TCĐ: $x=2$.\r\n(Tổng cộng 2 TCĐ)\r\nSố đường tiệm cận là: 2 (ngang) + 2 (đứng) = 4.