Hàm số $y={{\log }_{3}}\left( {{x}^{2}}-2x \right)$ nghịch biến trên khoảng $\left( -\infty ;a \right)$ có độ dài lớn nhất

Hàm số $y={{\log }_{3}}\left( {{x}^{2}}-2x \right)$ nghịch biến trên khoảng $\left( -\infty ;a \right)$ có độ dài lớn nhất. Khi đó a bằng?
Đáp án: 0

Lời giải: Hàm số $y={{\log }_{3}}\left( {{x}^{2}}-2x \right)$ có tập xác định $D=\left( -\infty ;0 \right)\cup \left( 2;+\infty \right)$.
Ta có ${y}’=\dfrac{2x-2}{\left( {{x}^{2}}-2x \right)\ln 3}$. Khi đó ${y}’=0$ $\Leftrightarrow$ $x=1$.
Bảng biến thiên:

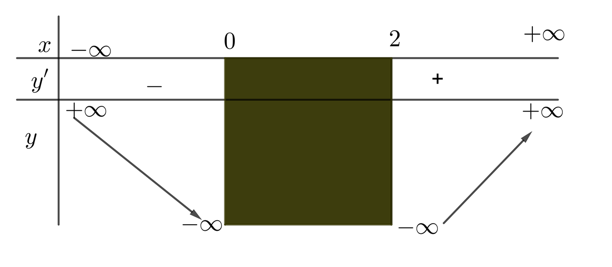
Dựa vào bảng biến thiên ta có hàm số $y$ nghịch biến trên $\left( -\infty ;0 \right)$.
Vậy $a=0$.