Một ông chủ nhà muốn làm một cái thang cứu hộ khi có nguy hiểm xảy ra

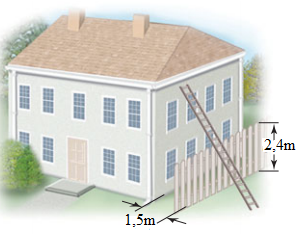
Một ông chủ nhà muốn làm một cái thang cứu hộ khi có nguy hiểm xảy ra. Ông ta muốn làm cái thang để nó đứng dưới đất vươn qua hàng rào tựa vào ngôi nhà (tham khảo hình vẽ). Với hàng rào cao 2,4 mét được đặt song song và cách bức tường của ngôi nhà một khoảng bằng 1,5 mét. Chiều dài ngắn nhất của cây thang bao nhiêu centimet (cm) để nó đứng dưới đất vươn qua hàng rào tựa vào ngôi nhà (làm tròn đến hàng đơn vị)?

Lời giải

Đáp án: $547$.

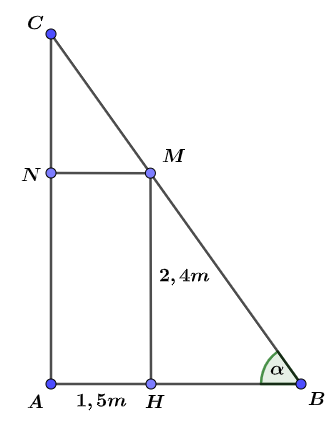
Gọi góc hợp bởi thang và mặt đất là $\alpha \,\,\left( 0<\alpha <\frac{\pi }{2} \right)$. Chiều dài thang là $BC=BM+MC$.

Tam giác vuông $MHB\,\,$có $BM=\frac{2,4}{\sin \alpha }$. Tam giác vuông $MNC\,\,$có $MC=\frac{1,5}{\cos \alpha }$.

$BC=BM+MC=\frac{2,4}{\sin \alpha }+\frac{1,5}{\cos \alpha }$. Xét hàm số $y=\frac{2,4}{\sin x}+\frac{1,5}{\cos x}$ với $x\in \left( 0;\frac{\pi }{2} \right)$

${y}’=\frac{-2,4.\cos x}{{{\sin }^{2}}x}+\frac{1,5.\sin x}{{{\cos }^{2}}x}=\frac{-2,4.{{\cos }^{3}}x+1,5.{{\sin }^{3}}x}{{{\sin }^{2}}x.{{\cos }^{2}}x}$,

${y}’=0\Leftrightarrow 2,4.{{\cos }^{3}}x=1,5.{{\sin }^{3}}x\Leftrightarrow {{\tan }^{3}}x=\frac{2,4}{1,5}\Leftrightarrow \tan x=\sqrt[3]{\frac{8}{5}}$, do $x\in \left( 0;\frac{\pi }{2} \right)$nên $x\approx 0,863$rad

Ta có bảng biến thiên

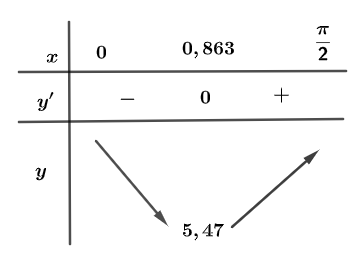
Dựa vào bảng biến thiên, ta thấy chiều dài thang bé nhất xấp xỉ 5,47 mét hay 547 cm.