Người ta muốn lắp một ống dẫn dầu từ nhà máy lọc dầu ở vị trí $A$ đến kho chứa dầu đặt ở vị trí $B$ qua một con sông rộng $2$km, dài $6$km

Người ta muốn lắp một ống dẫn dầu từ nhà máy lọc dầu ở vị trí $A$ đến kho chứa dầu đặt ở vị trí $B$ qua một con sông rộng $2$km, dài $6$km. Chi phí lắp đặt đường ống dẫn dầu trên mặt đất để nối từ nhà máy lọc dầu đến trạm trung chuyển tại vị trí $P$ là $4$tỷ VNĐ/$1$km và chi phí lắp đặt đường ống dẫn dầu dưới dòng sông để nối từ $P$ đến kho chứa dầu tại vị trí $B$ là $8$tỷ VNĐ/$1$km (như hình vẽ)

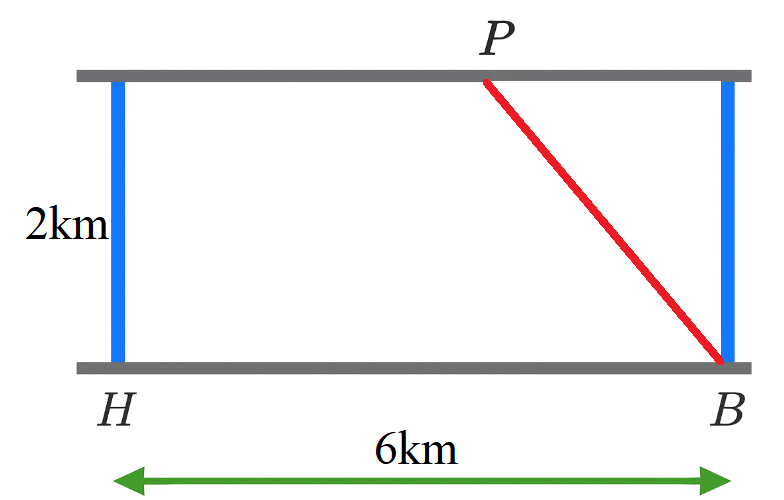
Hỏi chi phí lắp đặt ít nhất, cần đặt vị trí $P$ cách nhà máy lọc dầu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần trăm)

Lời giải

Đáp án: $4,85$.

Đặt $AP=x$ ($0\le x\le 6$, km).

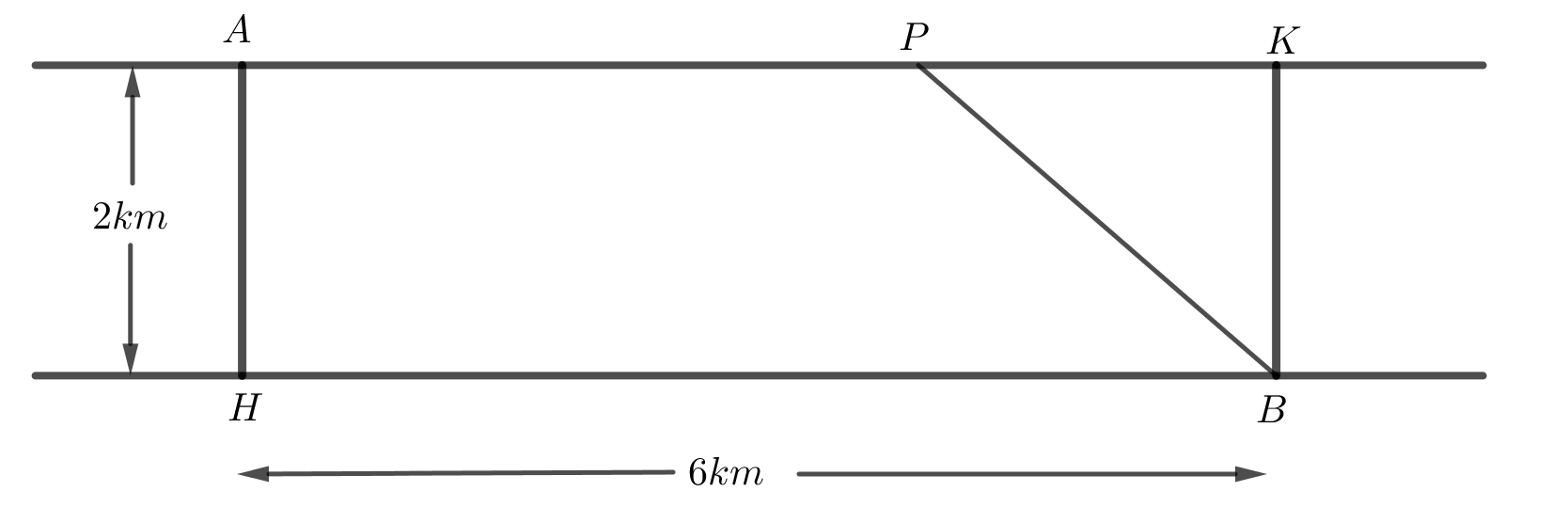
Khi đó, chiều dài quãng đường $PK=6-x$.

Tổng chi phí lắp đặt đường ống dẫn dầu là: $T=4x+8\sqrt{{{\left( 6-x \right)}^{2}}+{{2}^{2}}}$.

Ta có ${T}’\left( x \right)=4+8\frac{x-6}{\sqrt{{{x}^{2}}-12x+40}}$;

${T}’\left( x \right)=0\Leftrightarrow 4\sqrt{{{x}^{2}}-12x+40}+8x-48=0$

$\Leftrightarrow \sqrt{{{x}^{2}}-12x+40}=12-2x\left( K:0<x\le 6 \right)$

$\Leftrightarrow 3{{x}^{2}}-36x+104=0\Leftrightarrow x=\frac{18\pm 2\sqrt{3}}{3}$

Kết hợp đk ta thấy: $x=\frac{18-2\sqrt{3}}{3}\approx 4,85$ là nghiệm của pt.

${T}’\left( x \right)<0\Leftrightarrow 4\sqrt{{{x}^{2}}-12x+40}+8x-48<0$

$\Leftrightarrow \sqrt{{{x}^{2}}-12x+40}<12-2x$

$\Leftrightarrow \left\{ \begin{matrix}

12-2x>0\text{ } \\

{{x}^{2}}-12x+40<144-48x+4{{x}^{2}} \\

\end{matrix} \right.$$\Leftrightarrow \left\{ \begin{matrix}

0<x<6\text{ } \\

3{{x}^{2}}-36x+104>0 \\

\end{matrix} \right.$

$\Leftrightarrow 0<x<\frac{18-2\sqrt{3}}{3}\approx 4,85$

Từ đây ta có bảng biến thiên

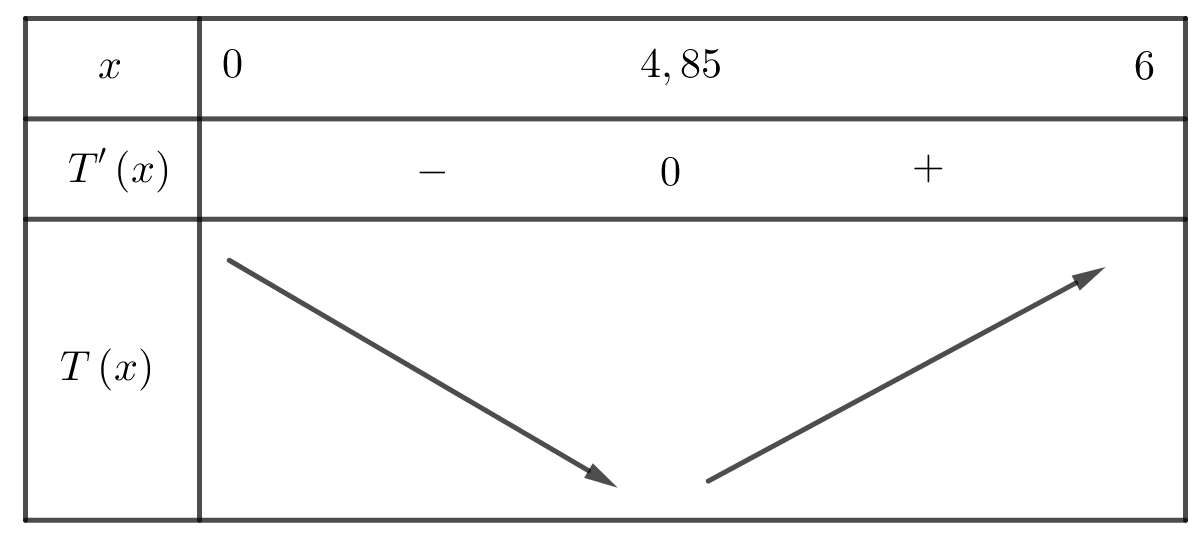
Từ bảng biến thiên ta suy ra chi phí thấp nhất khi $x=4,85$.