Trong một cửa hàng, nhà quản lý dự định treo một đồ trang trí trên cao

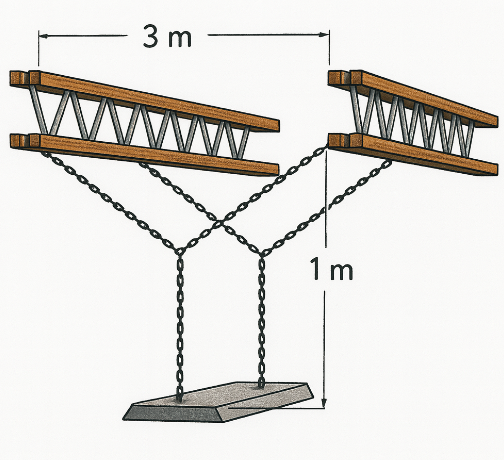
Trong một cửa hàng, nhà quản lý dự định treo một đồ trang trí trên cao. Vật trang trí được đặt trên giá đỡ nằm dưới thanh treo 1m. Biết khoảng cách giữa hai thanh treo là 3m. Biết tổng độ dài nhỏ nhất của các đoạn dây xích là $a+b\sqrt{c}$ (trong đó ${a,b,c }$ là các số tự nhiên). Tính _{$a\text{ }-b-c.$}

Lời giải

Đáp án: $-4$.

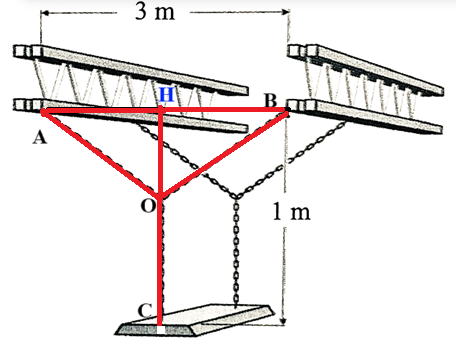
Đặt $OH=x\left( 0\le x\le 1 \right)$ ta có $OA=OB=\sqrt{{{\left( \frac{3}{2} \right)}^{2}}+{{x}^{2}}}=\sqrt{\frac{9}{4}+{{x}^{2}}}$ và $OC=1-x$.

Tổng độ dài các dây xích là

$L\left( x \right)=2\left( OA+OB+OC \right)$ $=2\left( 2\sqrt{\frac{9}{4}+{{x}^{2}}}+1-x \right)$$=4\sqrt{\frac{9}{4}+{{x}^{2}}}+2-2x$.

${L}’\left( x \right)=\frac{4x}{\sqrt{\frac{9}{4}+{{x}^{2}}}}-2=0$$\Leftrightarrow \sqrt{\frac{9}{4}+{{x}^{2}}}=2x\Leftrightarrow \left\{ \begin{align}

& x\ge 0 \\

& 4{{x}^{2}}={{x}^{2}}+\frac{9}{4} \\

\end{align} \right.$ $\Leftrightarrow x=\frac{\sqrt{3}}{2}.$

Bảng biến thiên

Vậy chiều dài tối thiểu của dây xích là $L\left( \frac{\sqrt{3}}{2} \right)=2+3\sqrt{3}$.

Suy ra $\left\{ \begin{align}

& a=2 \\

& b=3 \\

& c=3 \\

\end{align} \right.\Rightarrow a-b-c=-4$.