Hình bên mô tả một mặt cắt ngang của một tòa nhà cao tầng

Hình bên mô tả một mặt cắt ngang của một tòa nhà cao tầng. Một chiếc thang từ xe cứu hỏa lên đến mặt tường phía trước của tòa nhà phải vượt qua phần mái che cao hơn 10m so với mặt đất và vùng mái này nhô ra 12m so với tường. 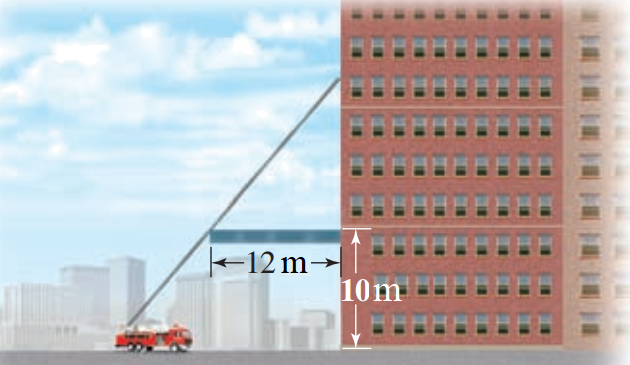Giả sử, độ cao của xe cứu hỏa là không đáng kể, hãy tìm độ dài ngắn nhất của chiếc thang để các lính cứu hỏa có thể thực hiện nhiệm vụ này (làm tròn kết quả đến hàng phần mười)

Lời giải

Đặt ${L}$ là độ dài của chiếc thang, và ${\theta}$ là góc tạo bởi thang với phương ngang, gọi ${d_1}$ là đoạn thẳng từ mặt đất lên tới mái hiên, ${d_2}$ là đoạn từ mái hiên tới tường. Khi đó $L={{d}_{1}}+{{d}_{2}}=\frac{10}{\sin \theta }+\frac{12}{\cos \theta }$

Miền xác định của ${L(\theta)}$ là ${\theta \in\left(0, \frac{\pi}{2}\right)}$.

Hàm số $f(\theta )=\frac{10}{\sin \theta }+\frac{12}{\cos \theta }$ liên tục trên ${\left(0, \frac{\pi}{2}\right)}$.

Ta tính đạo hàm ${{f}^{\prime }}(\theta )=-\frac{10}{\sin \theta }\cot \theta +\frac{12}{\cos \theta }\tan \theta $

Giải ${f^{\prime}(\theta)=0}$:

$\frac{12}{\cos \theta }\tan \theta =\frac{10}{\sin \theta }\cot \theta \Rightarrow 12\frac{1}{\cos \theta }\frac{\sin \theta }{\cos \theta }=10\frac{1}{\sin \theta }\frac{\cos \theta }{\sin \theta }\Leftrightarrow \frac{{{\sin }^{3}}\theta }{{{\cos }^{3}}\theta }=\frac{10}{12}\Leftrightarrow {{\tan }^{3}}\theta =\frac{5}{6}$.

Do đó $\theta \approx 0,76rad$

Lập bảng xét dấu ${f^{\prime}(\theta)}$, ta thấy đây là điểm cực tiểu duy nhất trên ${\left(0, \frac{\pi}{2}\right)}$.

Cuối cùng $f(0,76)\approx 31,07$nên độ dài thang ngắn nhất cần thiết là $31,1m\text{. }$