Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

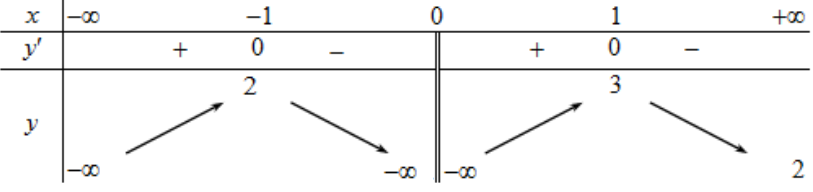
a) Hàm số $y=f\left( x \right)$ nghịch biến trên $\left( 0;1 \right)$.

b) Hàm số $y=f\left( x \right)$ đồng biến trên $\left( -\infty ;-1 \right)$.

c) Hàm số $y=f\left( x \right)$ có 2 điểm cực trị.

d) Giá trị lớn nhất của $g\left( x \right)=f\left( x \right)+\sin x$ trên đoạn $\left[ -\dfrac{\pi }{2};-1 \right]$ là $1$.

Lời giải:

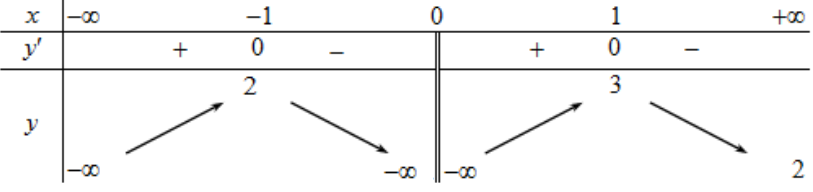
(Sai) Hàm số $y=f\left( x \right)$ nghịch biến trên $\left( 0;1 \right)$.
(Vì): Dựa vào bảng biến thiên.
(Đúng) Hàm số $y=f\left( x \right)$ đồng biến trên $\left( -\infty ;-1 \right)$.
(Vì): Dựa vào bảng biến thiên, ta thấy ${f}'(x) {>} 0$ trên $\left( -\infty ;-1 \right)$, suy ra hàm số đồng biến trên $\left( -\infty ;-1 \right)$.
(Đúng) Hàm số $y=f\left( x \right)$ có 2 điểm cực trị.
(Vì): Dựa vào bảng biến thiên, ${f}'(x)$ đổi dấu tại $x=-1$ và $x=1$, và hàm số xác định tại các điểm này. Tại $x=0$, hàm số không xác định nên không phải điểm cực trị. Vậy hàm số có 2 điểm cực trị.
(Sai) Giá trị lớn nhất của $g\left( x \right)=f\left( x \right)+\sin x$ trên đoạn $\left[ -\dfrac{\pi }{2};-1 \right]$ là $1$.
(Vì): Hàm số $g\left( x \right)=f\left( x \right)+\sin x$ liên tục trên đoạn $\left[ -\dfrac{\pi }{2};-1 \right]$ và ${g}’\left( x \right)={f}’\left( x \right)+\cos x {>} 0,\forall x\in \left[ -\dfrac{\pi }{2};-1 \right]$. Suy ra $g\left( x \right)$ đồng biến trên $\left[ -\dfrac{\pi }{2};-1 \right]$. Vậy $\max\limits_{\left[ -\frac{\pi }{2};-1 \right]}g\left( x \right)=g(-1)=f(-1)+\sin (-1)=2-\sin 1$.