Cho hình hộp chữ nhật $ABCD

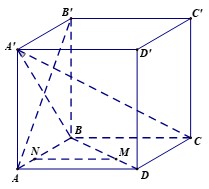
Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}’$ có $AB=x$, $AD=1$. $\widehat{B{A}’C}=30{}^\circ$. $M$ là điểm di chuyển trên đoạn $BD$.

a) Giá trị lớn nhất của góc giữa hai đường thẳng $A{B}’$ và $BA’$ là ${{90}^{o}}$.

b) Giá trị lớn nhất của khoảng cách từ $M$ đến mặt phẳng $(ABB’A’)$ là $\sqrt{2}$.

c) Giá trị lớn nhất ${{V}_{max}}$ của thể tích khối hộp $ABCD.{A}'{B}'{C}'{D}’$ là ${{V}_{max}}=\dfrac{3}{2}$.

d) Giá trị lớn nhất của tan góc giữa đường thẳng $A{B}’$ và mặt phẳng $\left( BC{C}'{B}’ \right)$ không tồn tại.

Lời giải:

(Đúng) Giá trị lớn nhất của góc giữa hai đường thẳng $A{B}’$ và $BA’$ là ${{90}^{o}}$
(Vì): Gọi $\theta$ là góc giữa $A{B}’$ và $BA’$. Ta có $AB=x$, $AD=1$, và $h=AA’=\sqrt{3-x^2}$ (từ việc $\triangle A’BC$ vuông tại $B$, $A’B = BC/\tan(30^\circ) = 1/(1/\sqrt{3}) = \sqrt{3}$, và $A’B^2 = AB^2+AA’^2 \Rightarrow 3=x^2+h^2$). Ta có $\vec{AB’} = (x,0,h)$ và $\vec{BA’} = (-x,0,h)$. $\cos\theta = \dfrac{|\vec{AB’} \cdot \vec{BA’}|}{|\vec{AB’}| |\vec{BA’}|} = \dfrac{|-x^2+h^2|}{\sqrt{x^2+h^2}\sqrt{x^2+h^2}} = \dfrac{|h^2-x^2|}{3}$. Thay $h^2=3-x^2$, ta có $\cos\theta = \dfrac{|(3-x^2)-x^2|}{3} = \dfrac{|3-2x^2|}{3}$. Để góc $\theta$ lớn nhất thì $\cos\theta$ phải nhỏ nhất. Giá trị nhỏ nhất của $\cos\theta$ là $0$ khi $3-2x^2=0 \Rightarrow x^2=3/2$. Khi đó $\theta=90^\circ$.
(Sai) Giá trị lớn nhất của khoảng cách từ $M$ đến mặt phẳng $(ABB’A’)$ là $\sqrt{2}$.
(Vì): Khoảng cách từ $M$ đến mặt phẳng $(ABB’A’)$ là $d(M, (ABB’A’))$. Đặt $A$ là gốc tọa độ $(0,0,0)$, $AB$ trên trục $Ox$, $AD$ trên trục $Oy$, $AA’$ trên trục $Oz$. Khi đó mặt phẳng $(ABB’A’)$ là mặt phẳng $xOz$ (phương trình $y=0$). Điểm $M$ di chuyển trên đoạn $BD$. Tọa độ điểm $B(x,0,0)$ và $D(0,1,0)$. Một điểm $M(x_M, y_M, z_M)$ trên đoạn $BD$ sẽ có $z_M=0$. Phương trình đường thẳng $BD$ là $\dfrac{x_M}{x} + \dfrac{y_M}{1} = 1$. Khoảng cách từ $M(x_M, y_M, 0)$ đến mặt phẳng $(ABB’A’)$ là $|y_M|$. Vì $M$ thuộc đoạn $BD$, giá trị $y_M$ nằm trong khoảng $[0, AD]$ hay $[0,1]$. Vậy giá trị lớn nhất của khoảng cách này là $1$, không phải $\sqrt{2}$.
(Đúng) Giá trị lớn nhất ${{V}_{max}}$ của thể tích khối hộp $ABCD.{A}'{B}'{C}'{D}’$ là ${{V}_{max}}=\dfrac{3}{2}$
(Vì): Thể tích khối hộp là $V = AB \cdot AD \cdot AA’ = x \cdot 1 \cdot h$. Với $h=\sqrt{3-x^2}$, ta có $V = x\sqrt{3-x^2}$. Để tìm giá trị lớn nhất của $V$, ta tìm giá trị lớn nhất của $V^2 = x^2(3-x^2)$. Đặt $t=x^2$, với $x \in (0,\sqrt{3})$, thì $t \in (0,3)$. Ta có $V^2 = t(3-t)$. Áp dụng bất đẳng thức AM-GM cho hai số dương $t$ và $3-t$, ta có $t(3-t) \le \left(\dfrac{t+(3-t)}{2}\right)^2 = \left(\dfrac{3}{2}\right)^2 = \dfrac{9}{4}$. Dấu “=” xảy ra khi $t = 3-t \Rightarrow 2t=3 \Rightarrow t=3/2$. Vậy ${{V}_{max}^2} = \dfrac{9}{4} \Rightarrow {{V}_{max}} = \sqrt{\dfrac{9}{4}} = \dfrac{3}{2}$.
(Đúng) Giá trị lớn nhất của tan góc giữa đường thẳng $A{B}’$ và mặt phẳng $\left( BC{C}'{B}’ \right)$ không tồn tại.
(Vì): Gọi $\alpha$ là góc giữa đường thẳng $A{B}’$ và mặt phẳng $\left( BC{C}'{B}’ \right)$. Ta có $AB \perp BC$ và $AB \perp BB’$ nên $AB \perp (BCC’B’)$. Do đó, hình chiếu của $AB’$ lên mặt phẳng $(BCC’B’)$ là $BB’$. Góc $\alpha$ chính là góc $\widehat{AB’B}$. Trong tam giác vuông $ABB’$ (vuông tại $B$), ta có $\tan\alpha = \dfrac{AB}{BB’} = \dfrac{x}{h}$. Với $h=\sqrt{3-x^2}$, ta có $\tan\alpha = \dfrac{x}{\sqrt{3-x^2}}$. Xét hàm số $f(x) = \dfrac{x}{\sqrt{3-x^2}}$ với $x \in (0, \sqrt{3})$. Khi $x \to \sqrt{3}^-$, thì $3-x^2 \to 0^+$, do đó $\sqrt{3-x^2} \to 0^+$. Khi đó $\lim_{x \to \sqrt{3}^-} \tan\alpha = \lim_{x \to \sqrt{3}^-} \dfrac{x}{\sqrt{3-x^2}} = \dfrac{\sqrt{3}}{0^+} = +\infty$. Vậy, giá trị lớn nhất của tan góc này không tồn tại.