Một tấm nhôm hình vuông cạnh $120cm$. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( cm \right)$, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp.
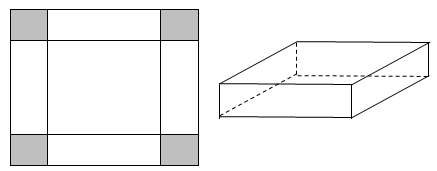
a) Thể tích khối hộp nhận được khi tính theo $x$ là $V=x{{\left( 120-2x \right)}^{2}}$.
b) Để hộp nhận được có thể tích lớn nhất thì $x=10\left( cm \right)$.
c) Khi $x=10cm$ thì thể tích của khối hộp nhận được là $1\left( {{m}^{3}} \right)$.
d) Hộp nhận được có thể tích lớn nhất là $100\left( d{{m}^{3}} \right)$.
Lời giải: Điều kiện: $0{<}x{
Khi $x=10cm$ thể tích khối hộp nhận được là $V=100000\left( c{{m}^{3}} \right)=0,1\left( {{m}^{3}} \right)$.Với $x\in \left( 0;60 \right)$
ta có: ${f}’\left( x \right)=12{{x}^{2}}-960x+14400\Rightarrow {f}’\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l} x=60\left( l \right) \\ x=20 \end{array} \right.$.
Bảng biến thiên
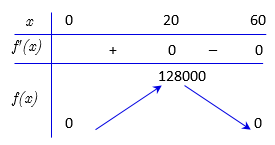
Suy ra $V$ đạt giá trị lớn nhất khi $x=20\left( cm \right)$. ${{V}_{\max }}=128000\left( c{{m}^{3}} \right)=128\left( d{{m}^{3}} \right)(Đúng) Thể tích khối hộp nhận được khi tính theo$x$là$V=x{{\left( 120-2x \right)}^{2}}$.(Vì): Điều kiện:$0{<}x{
Để lại một bình luận