Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng

Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm $h\left( t \right)=-0,01{{t}^{3}}+1,1{{t}^{2}}-30t+250$, trong đó $t$ là thời gian tính bằng giây và $h$ là độ cao tính bằng kilômét.Các mệnh đề sau đúng hay sai?

a) Xét thời điểm $0\le t\le 50$ thì tại thời điểm $t\approx 18$ giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.

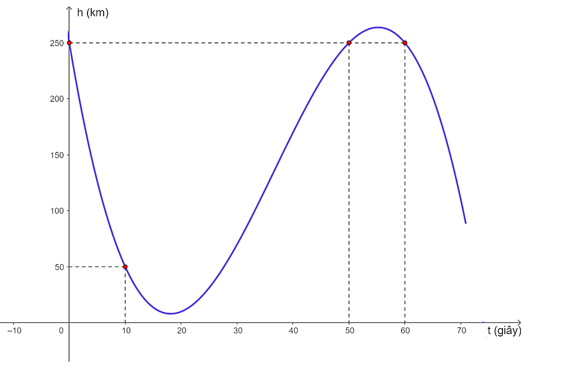
b) Đồ thị của hàm số $y=h\left( t \right)$ với $0\le t\le 70$ (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km) KHÔNG đi qua điểm $(10; 50)$.

c) Gọi $v\left( t \right)$ là vận tốc tức thời của con tàu ở thời điểm $t$ (giây) kể từ khi đốt cháy các tên lửa hãm với $0\le t\le 50$. Vận tốc tức thời của con tàu tại thời điểm $t=25$ (giây) là 5,25 km/s.

d) Tại thời điểm $t=25$ (giây), vận tốc tức thời của con tàu đang tăng.

Lời giải: Xét hàm số $h\left( t \right)=-0,01{{t}^{3}}+1,1{{t}^{2}}-30t+250$ với $t\in \left[ 0;50 \right]$
Ta có $h’\left( t \right)=-0,03{{t}^{2}}+2,2t-30$
$\Rightarrow h’\left( t \right)=0\Leftrightarrow -0,03{{t}^{2}}+2,2t-30=0\Leftrightarrow t\approx 18$ (với $t\in \left[ 0;50 \right]$ )
Ta có:
$\begin{array}{l}h\left( 0 \right)=250 \\h\left( 18 \right)=8,08 \\h\left( 50 \right)=250 \\\end{array}$
Do đó, $\min\limits_{\left[ 0;50 \right]}h\left( t \right)=8,08$ tại $t\approx 18$.
Vậy tại thời điểm $t\approx 18$ giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.Suy ra mệnh đề đúng.Đúng. Xét hàm số $h\left( t \right)=-0,01{{t}^{3}}+1,1{{t}^{2}}-30t+250$ với $t\in \left[ 0;70 \right]$
Ta có $h’\left( t \right)=-0,03{{t}^{2}}+2,2t-30$
$\Rightarrow h’\left( t \right)=0\Leftrightarrow -0,03{{t}^{2}}+2,2t-30=0\Leftrightarrow \left[ \begin{array}{l}t\approx 18 \\t\approx 55 \\\end{array} \right.$
Bảng biến thiên của hàm số h(t) như sau:

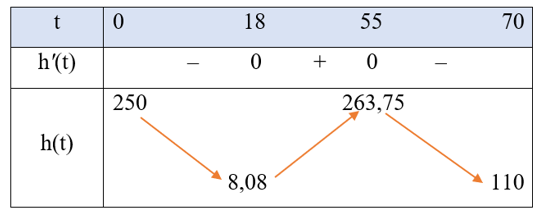
Trên khoảng $(0; 70)$, đồ thị hàm số h(t) đi qua các điểm $(0; 250)$, $(10; 50)$, $(50; 250)$ và $(60; 250)$.

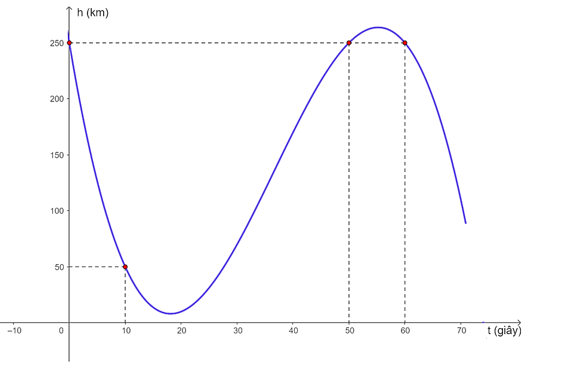
Suy ra mệnh đề đúng.Sai. Ta có $v\left( t \right)$ là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với $0\le t\le 50$.
Khi đó $v\left( t \right)=h’\left( t \right)=-0,03{{t}^{2}}+2,2t-30$ với $t\in \left[ 0;50 \right]$
$v\left( 25 \right)=-0,03\cdot {{25}^{2}}+2,2\cdot 25-30=6,25$ (km/s).Suy ra mệnh đề sai.Sai. Tại thời điểm $t=25$ (giây), lúc đó $t\in \left[ 18;55 \right]$, căn cứ vào bảng biến thiên ở câu b), ta thấy rằng $h’\left( t \right){>}0$, tức là $v\left( t \right){>}0$, vậy vận tốc tức thời của con tàu đang tăng trở lại.
Suy ra mệnh đề sai.
(Đúng) Xét thời điểm $0\le t\le 50$ thì tại thời điểm $t\approx 18$ giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.
(Vì): Xét hàm số $h\left( t \right)=-0,01{{t}^{3}}+1,1{{t}^{2}}-30t+250$ với $t\in \left[ 0;50 \right]$
Ta có $h’\left( t \right)=-0,03{{t}^{2}}+2,2t-30$
$\Rightarrow h’\left( t \right)=0\Leftrightarrow -0,03{{t}^{2}}+2,2t-30=0\Leftrightarrow t\approx 18$ (với $t\in \left[ 0;50 \right]$ )
Ta có:
$\begin{array}{l}h\left( 0 \right)=250 \\h\left( 18 \right)=8,08 \\h\left( 50 \right)=250 \\\end{array}$
Do đó, $\min\limits_{\left[ 0;50 \right]}h\left( t \right)=8,08$ tại $t\approx 18$.
Vậy tại thời điểm $t\approx 18$ giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.Suy ra mệnh đề đúng.
(Sai) Đồ thị của hàm số $y=h\left( t \right)$ với $0\le t\le 70$ (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km) KHÔNG đi qua điểm $(10; 50)$.

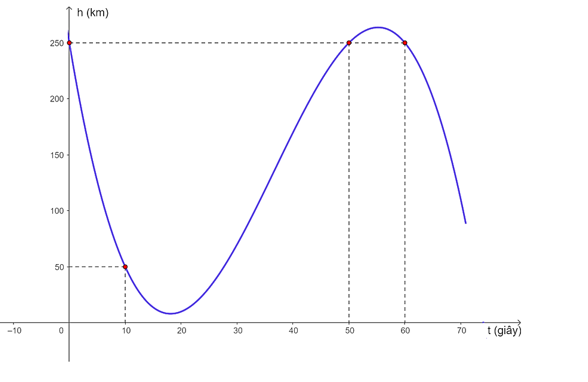
(Vì): Đúng. Xét hàm số $h\left( t \right)=-0,01{{t}^{3}}+1,1{{t}^{2}}-30t+250$ với $t\in \left[ 0;70 \right]$
Ta có $h’\left( t \right)=-0,03{{t}^{2}}+2,2t-30$
$\Rightarrow h’\left( t \right)=0\Leftrightarrow -0,03{{t}^{2}}+2,2t-30=0\Leftrightarrow \left[ \begin{array}{l}t\approx 18 \\t\approx 55 \\\end{array} \right.$
Bảng biến thiên của hàm số h(t) như sau:

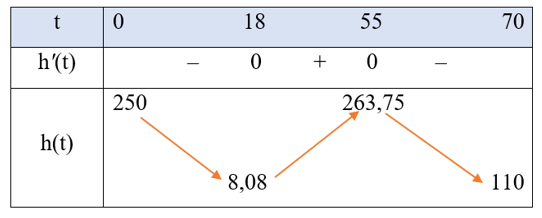
Trên khoảng $(0; 70)$, đồ thị hàm số h(t) đi qua các điểm $(0; 250)$, $(10; 50)$, $(50; 250)$ và $(60; 250)$.

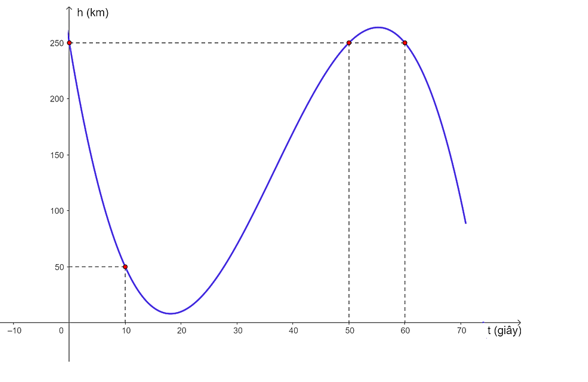
Suy ra mệnh đề đúng.
(Sai) Gọi $v\left( t \right)$ là vận tốc tức thời của con tàu ở thời điểm $t$ (giây) kể từ khi đốt cháy các tên lửa hãm với $0\le t\le 50$. Vận tốc tức thời của con tàu tại thời điểm $t=25$ (giây) là 5,25 km/s.
(Vì): Sai. Ta có $v\left( t \right)$ là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với $0\le t\le 50$.
Khi đó $v\left( t \right)=h’\left( t \right)=-0,03{{t}^{2}}+2,2t-30$ với $t\in \left[ 0;50 \right]$
$v\left( 25 \right)=-0,03\cdot {{25}^{2}}+2,2\cdot 25-30=6,25$ (km/s).Suy ra mệnh đề sai.
(Đúng) Tại thời điểm $t=25$ (giây), vận tốc tức thời của con tàu đang tăng.
(Vì): Sai. Tại thời điểm $t=25$ (giây), lúc đó $t\in \left[ 18;55 \right]$, căn cứ vào bảng biến thiên ở câu b), ta thấy rằng $h’\left( t \right){>}0$, tức là $v\left( t \right){>}0$, vậy vận tốc tức thời của con tàu đang tăng trở lại.
Suy ra mệnh đề sai.