Đường dây điện $110KV$ kéo từ trạm phát trong đất liền ra Côn Đảo . Biết $BC=60km$, $AB=100km$, góc $\widehat{ABC}=90{}^\circ$, như hình vẽ. Mỗi $km$ dây điện dưới nước chi phí là $5000USD$, chi phí cho mỗi $km$ dây điện trên bờ là $3000USD$. Đặt $x=AG$.
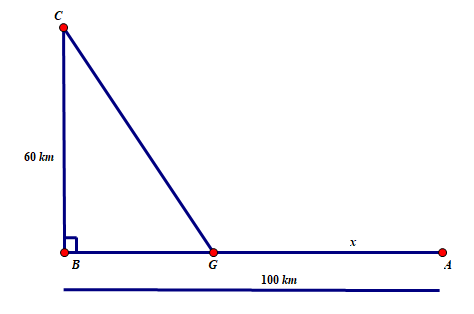
a) Khi $x=20km$ thì đường dây điện nối từ $C$ về $G$ dài $100km$.
b) Khi $x=20km$ thì tổng chi phí mắc điện là $550.000USD$.
c) Tổng chi phí mắc điện nhỏ nhất là $545.000USD$.
d) Tổng chi phí mắc điện nhỏ nhất khi $x=55km$.
Lời giải:
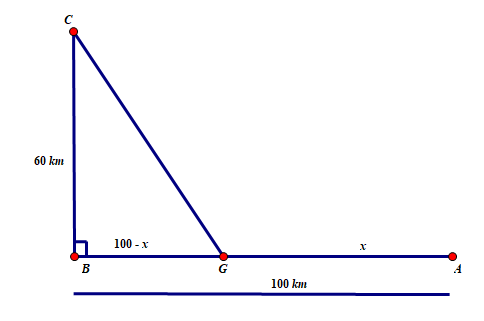
Có $AG=x\Rightarrow BG=100-x$ với $0\le x\le 100$.
Xét tam giác $CBG$ vuông tại $B$ có $CG=\sqrt{C{{B}^{2}}+B{{G}^{2}}}=\sqrt{3600+{{\left( 100-x \right)}^{2}}}$.
Khi $x=20km\Rightarrow CG=100km$.Chi phí tiền mắc điện là $f\left( x \right)=3000x+5000\cdot\sqrt{3600+{{\left( 100-x \right)}^{2}}}$
Khi $x=20km\Rightarrow CG=100km$ và tổng chi phí mắc điện là $T=f\left( 20 \right)=560.000USD$.Để chi phí mắc điện ít nhất thì $f\left( x \right)$ đạt giá trị nhỏ nhất.
Ta có ${f}’\left( x \right)=3000-5000\dfrac{\left( 100-x \right)}{\sqrt{3600+{{\left( 100-x \right)}^{2}}}}$
$\Rightarrow {f}’\left( x \right)=0 \Leftrightarrow 3000=5000\dfrac{\left( 100-x \right)}{\sqrt{3600+{{\left( 100-x \right)}^{2}}}}\Leftrightarrow x=55$ hoặc $x=145$ (loại).
Ta có $f\left( 0 \right)=583095,1895\text{USD}$, $f\left( 55 \right)=540.000USD$, $f\left( 100 \right)=600.000\text{USD}$.
Vậy chi phí mắc điện nhỏ nhất khi $x=55km$. Chi phí mắc điện nhỏ nhất là $540.000USD$.
(Đúng) Khi $x=20km$ thì đường dây điện nối từ $C$ về $G$ dài $100km$.
(Vì): Từ lời giải, khi $x=20km$ thì $CG=100km$.
(Sai) Khi $x=20km$ thì tổng chi phí mắc điện là $550.000USD$.
(Vì): Từ lời giải, khi $x=20km$ thì tổng chi phí mắc điện là $560.000USD$, không phải $550.000USD$.
(Sai) Tổng chi phí mắc điện nhỏ nhất là $545.000USD$.
(Vì): Từ lời giải, tổng chi phí mắc điện nhỏ nhất là $540.000USD$, không phải $545.000USD$.
(Đúng) Tổng chi phí mắc điện nhỏ nhất khi $x=55km$.
(Vì): Từ lời giải, tổng chi phí mắc điện nhỏ nhất khi $x=55km$.
