Một tấm bìa cứng hình chữ nhật có kích thước $\text{3}m\times 8m$

Một tấm bìa cứng hình chữ nhật có kích thước $\text{3}m\times 8m$. Người ta cắt mỗi góc của tấm bìa một hình vuông có cạnh là $x$ để tạo ra hình hộp chữ nhật không nắp (như hình vẽ). Xét tính đúng, sai của các mệnh đề sau:

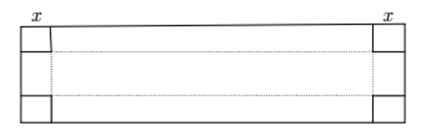
a) Điều kiện của $x$ là $\text{0}{<}x{<}\dfrac{\text{3}}{2}$.

b) Diện tích mặt đáy của chiếc hộp là $\left( 8-\text{2}x \right)\left( \text{3}-\text{2}x \right)$.

c) Thể tích của chiếc hộp là ${{\left( 8-\text{2}x \right)}^{\text{2}}}\left( \text{3}-\text{2}x \right)$.

d) Với $x=1\left( m \right)$ thì chiếc hộp có thể tích lớn nhất.

Lời giải:

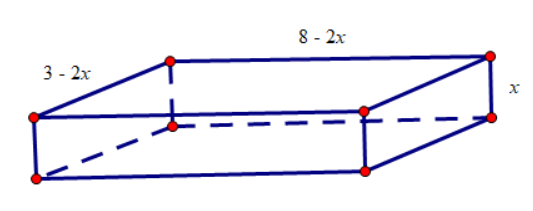
[NB] Ta có chiều dài, chiều rộng, chiều cao của chiếc hộp lần lượt là $8-\text{2}x;\text{3}-\text{2}x;x$.
Suy ra điều kiện của $x$ là $\text{0}{<}x{
[TH] Đáy của chiếc hộp là hình chữ nhật có diện tích là $S=\left( 8-\text{2}x \right)\left( \text{3}-\text{2}x \right)$. Vậy b) Đúng.
[TH] Thể tích của chiếc hộp là: $V=x\left( 8-\text{2}x \right)\left( \text{3}-\text{2}x \right)$. Vậy c) Sai.[VD,VDC]
Xét hàm số: $V\left( x \right)=x\left( 3-2x \right)\left( 8-2x \right)=4{{x}^{3}}-22{{x}^{2}}+24x$ trên $\left( \text{0;}\dfrac{\text{3}}{2} \right)$.
Ta có: ${V}’\left( x \right)=12{{x}^{2}}-44x+24=4\left( 3{{x}^{2}}-11x+6 \right)$.
Khi đó: ${V}’\left( x \right)=0\Leftrightarrow \left[ \begin{array}{l}x=3 \\x=\dfrac{2}{3} \\\end{array} \right.$.
Bảng biến thiên:

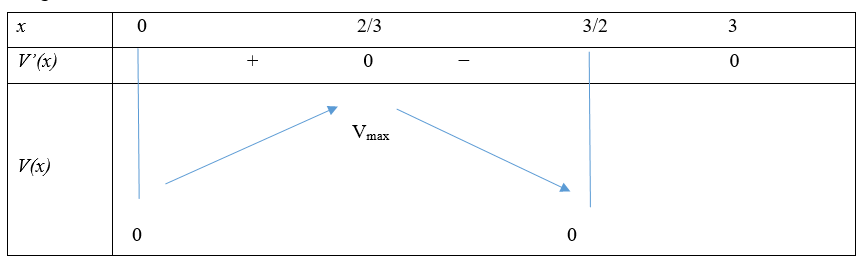
Từ BBT ta thấy hàm số đạt giá trị lớn nhất trên $\left( \text{0;}\dfrac{\text{3}}{2} \right)$ khi $x=\dfrac{2}{3}$. Vậy d) Đúng
(Đúng) Điều kiện của $x$ là $\text{0}{<}x{<}\dfrac{\text{3}}{2}$.
(Đúng) Diện tích mặt đáy của chiếc hộp là $\left( 8-\text{2}x \right)\left( \text{3}-\text{2}x \right)$.
(Sai) Thể tích của chiếc hộp là ${{\left( 8-\text{2}x \right)}^{\text{2}}}\left( \text{3}-\text{2}x \right)$.
(Sai) Với $x=1\left( m \right)$ thì chiếc hộp có thể tích lớn nhất
(Vì): Từ BBT ta thấy hàm số đạt giá trị lớn nhất trên $\left( \text{0;}\dfrac{\text{3}}{2} \right)$ khi $x=\dfrac{2}{3}$.