Giả sử một công ty du lịch bán tour với giá là $x$ (triệu đồng)/khách thì doanh thu sẽ được biểu diễn qua hàm số $f(x)=-200{{x}^{2}}+550x$

Giả sử một công ty du lịch bán tour với giá là $x$ (triệu đồng)/khách thì doanh thu sẽ được biểu diễn qua hàm số $f(x)=-200{{x}^{2}}+550x$. Công ty phải bán giá tour cho một khách là bao nhiêu để doanh thu từ tua xuyên Việt là lớn nhất (làm tròn tới hàng phần trăm).
Đáp án: 1,38

Lời giải: Doanh thu là $f(x)=-200{{x}^{2}}+550x$.
Ta có ${f}’\left( x \right)=-400x+550$. ${f}’\left( x \right)=0\Leftrightarrow x=\dfrac{11}{8}$.
Bảng biến thiên

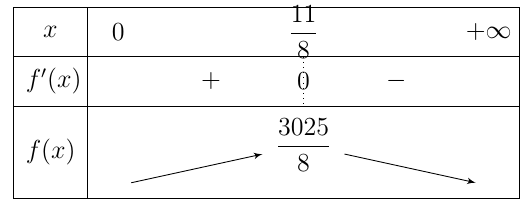
Dựa vào bảng biến thiên ta thấy $f\left( x \right)$ đạt giá trị lớn nhất khi $x=\dfrac{11}{8}=1,375$.
Vậy công ty cần bán tour với giá 1,38 triệu đồng/khách thì doanh thu sẽ cao nhất.