Câu hỏi: Một hộp nữ trang gồm phần thân là một hình hộp chữ nhật \(ABC D.EFGH\)làm bằng gỗ có \(AB = AE = 15{\rm{cm,}}\,BC = 20{\rm{cm}}\)và phần nắp là một phần của hình trụ làm bằng kính có tâm \(I\)của một đáy là trung điểm \(AB\), bán kính \(IE\), \(\widehat {EIF} = 60^\circ \) (như hình vẽ). Biết giá gỗ 2 triệu/m2, giá kính 1,5 triệu/m2. Giá vật liệu (lấy gần đúng đến … [Đọc thêm...] vềMột hộp nữ trang gồm phần thân là một hình hộp chữ nhật \(ABC D.EFGH\)làm bằng gỗ có \(AB = AE = 15{\rm{cm,}}\,BC = 20{\rm{cm}}\)và phần nắp là một phần của hình trụ làm bằng kính có tâm \(I\)của một đáy là trung điểm \(AB\), bán kính \(IE\), \(\widehat {EIF} = 60^\circ \) (như hình vẽ). Biết giá gỗ 2 triệu/m2, giá kính 1,5 triệu/m2. Giá vật liệu (lấy gần đúng đến hàng đơn vị) để làm một hộp nữ trang bằng bao nhiêu?
Trắc nghiệm Khối đa diện
Bên trong phòng khách một căn nhà có dạng hình lập phương, được ký hiệu ABC
D.A’B’C’D’ cạnh bằng 4(m). Người ta tiến hành trang trí ngôi nhà bằng cách gắn dây lụa nối từ điểm M đến N theo thứ tự trên AC và A’B sao cho \(AM = A’N = x\). Biết rằng chủ nhà muốn trang trí bằng dây lụa nhập khẩu giá 500.000 nghìn đồng 1m. Hỏi phải trang trí bằng cách nào cho đỡ tốn chi phí nhất? Chi phí mua dây là bao nhiêu?
Câu hỏi:
Bên trong phòng khách một căn nhà có dạng hình lập phương, được ký hiệu ABC
D.A’B’C’D’ cạnh bằng 4(m). Người ta tiến hành trang trí ngôi nhà bằng cách gắn dây lụa nối từ điểm M đến N theo thứ tự trên AC và A’B sao cho \(AM = A'N = x\). Biết rằng chủ nhà muốn trang trí bằng dây lụa nhập khẩu giá 500.000 nghìn đồng 1m. Hỏi phải trang trí bằng cách nào cho đỡ tốn chi … [Đọc thêm...] vềBên trong phòng khách một căn nhà có dạng hình lập phương, được ký hiệu ABC
D.A’B’C’D’ cạnh bằng 4(m). Người ta tiến hành trang trí ngôi nhà bằng cách gắn dây lụa nối từ điểm M đến N theo thứ tự trên AC và A’B sao cho \(AM = A’N = x\). Biết rằng chủ nhà muốn trang trí bằng dây lụa nhập khẩu giá 500.000 nghìn đồng 1m. Hỏi phải trang trí bằng cách nào cho đỡ tốn chi phí nhất? Chi phí mua dây là bao nhiêu?
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm \(A,B\)sao cho cung \(AB\)có số đo bằng \({120^ \circ }\). Người ta cắt khúc gỗ bởi một mặt phẳng đi qua \(A,B\)và tâm của hình trụ (tâm của hình trụ là trung điềm của đoạn nối tâm 2 đáy) để được thiết diện như hình vẽ.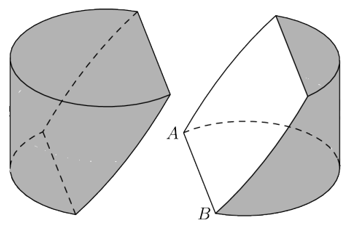 Biết diện tích \(S\)của thiết diện thu được có dạng\(S = a\pi + b\sqrt 3 \) . Tính \(P = a + b\)
Biết diện tích \(S\)của thiết diện thu được có dạng\(S = a\pi + b\sqrt 3 \) . Tính \(P = a + b\)
Câu hỏi:
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm \(A,B\)sao cho cung \(AB\)có số đo bằng \({120^ \circ }\). Người ta cắt khúc gỗ bởi một mặt phẳng đi qua \(A,B\)và tâm của hình trụ (tâm của hình trụ là trung điềm của đoạn nối tâm 2 đáy) để được thiết diện như hình vẽ.Biết diện tích \(S\)của thiết diện … [Đọc thêm...] vềMột khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm \(A,B\)sao cho cung \(AB\)có số đo bằng \({120^ \circ }\). Người ta cắt khúc gỗ bởi một mặt phẳng đi qua \(A,B\)và tâm của hình trụ (tâm của hình trụ là trung điềm của đoạn nối tâm 2 đáy) để được thiết diện như hình vẽ.Biết diện tích \(S\)của thiết diện thu được có dạng\(S = a\pi + b\sqrt 3 \) . Tính \(P = a + b\)
Cho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?
Câu hỏi:
Cho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?
A. \(1,03{{\rm{m}}^{\rm{3}}}\).
B. \(0,43{{\rm{m}}^{\rm{3}}}\).
C. … [Đọc thêm...] vềCho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?
Để chế tạo ra một cái đinh ốc, người ta đúc một vật bằng thép có dạng như hình vẽ bên. Trong đó, phần phía trên có dạng là một hình lăng trụ lục giác đều có chiều cao bằng 3cm và độ dài cạnh đáy bằng 4cm ; phần phía dưới có dạng một hình trụ có trục trùng với trục của lăng trụ đều phái trên, chiều cao bằng 12cm và chu vi đường tròn đáy bằng một nữa chu vi đáy của lăng trụ. Biết mỗi m3 thép có giá là m triệu đồng. Khi đó, giá nguyên liệu để làm một vật như trên gần nhất với kết quả nào dưới đây?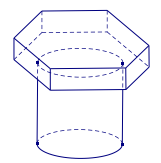
Câu hỏi:
Để chế tạo ra một cái đinh ốc, người ta đúc một vật bằng thép có dạng như hình vẽ bên. Trong đó, phần phía trên có dạng là một hình lăng trụ lục giác đều có chiều cao bằng 3cm và độ dài cạnh đáy bằng 4cm ; phần phía dưới có dạng một hình trụ có trục trùng với trục của lăng trụ đều phái trên, chiều cao bằng 12cm và chu vi đường tròn đáy bằng một nữa chu vi đáy của … [Đọc thêm...] vềĐể chế tạo ra một cái đinh ốc, người ta đúc một vật bằng thép có dạng như hình vẽ bên. Trong đó, phần phía trên có dạng là một hình lăng trụ lục giác đều có chiều cao bằng 3cm và độ dài cạnh đáy bằng 4cm ; phần phía dưới có dạng một hình trụ có trục trùng với trục của lăng trụ đều phái trên, chiều cao bằng 12cm và chu vi đường tròn đáy bằng một nữa chu vi đáy của lăng trụ. Biết mỗi m3 thép có giá là m triệu đồng. Khi đó, giá nguyên liệu để làm một vật như trên gần nhất với kết quả nào dưới đây?
Một hộp đựng phấn hình hộp chữ nhật có chiều dài \(30{\rm{cm}}\), chiều rộng \(5{\rm{cm}}\) và chiều cao \(6{\rm{cm}}\). Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là một một khối trụ có chiều cao \(h = 6{\rm{cm}}\)và bán kính đáy \(r = \frac{1}{2}{\rm{cm}}\). Hỏi có thể xếp được tối đa bao nhiêu viên phấn?
Câu hỏi: Một hộp đựng phấn hình hộp chữ nhật có chiều dài \(30{\rm{cm}}\), chiều rộng \(5{\rm{cm}}\) và chiều cao \(6{\rm{cm}}\). Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là một một khối trụ có chiều cao \(h = 6{\rm{cm}}\)và bán kính đáy \(r = \frac{1}{2}{\rm{cm}}\). Hỏi có thể xếp được tối đa bao nhiêu viên phấn? A. \(150\) viên. B. … [Đọc thêm...] vềMột hộp đựng phấn hình hộp chữ nhật có chiều dài \(30{\rm{cm}}\), chiều rộng \(5{\rm{cm}}\) và chiều cao \(6{\rm{cm}}\). Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là một một khối trụ có chiều cao \(h = 6{\rm{cm}}\)và bán kính đáy \(r = \frac{1}{2}{\rm{cm}}\). Hỏi có thể xếp được tối đa bao nhiêu viên phấn?
Một công ty sản xuất bút chì có dạng hình lăng trụ lục giác đều có chiều cao \(18\,{\rm{cm}}\) và đáy là hình lục giác nội tiếp đường tròn đường kính \(1\,{\mathop{\rm cm}\nolimits} \). Bút chì được cấu tạo từ hai thành phần chính là than chì và bột gỗ ép, than chì là một khối trụ ở trung tâm có đường kính \(\frac{1}{4}\,{\rm{cm}}\), giá thành \(540\) đồng\(/{{\mathop{\rm cm}\nolimits} ^3}\). Bột gỗ ép xung quanh có giá thành \(100\) đồng\(/{{\mathop{\rm cm}\nolimits} ^3}\). Tính giá của một cái bút chì được công ty bán ra biết giá nguyên vật liệu chiếm \(15,58\,\% \) giá thành sản phẩm.
Câu hỏi: Một công ty sản xuất bút chì có dạng hình lăng trụ lục giác đều có chiều cao \(18\,{\rm{cm}}\) và đáy là hình lục giác nội tiếp đường tròn đường kính \(1\,{\mathop{\rm cm}\nolimits} \). Bút chì được cấu tạo từ hai thành phần chính là than chì và bột gỗ ép, than chì là một khối trụ ở trung tâm có đường kính \(\frac{1}{4}\,{\rm{cm}}\), giá thành \(540\) … [Đọc thêm...] vềMột công ty sản xuất bút chì có dạng hình lăng trụ lục giác đều có chiều cao \(18\,{\rm{cm}}\) và đáy là hình lục giác nội tiếp đường tròn đường kính \(1\,{\mathop{\rm cm}\nolimits} \). Bút chì được cấu tạo từ hai thành phần chính là than chì và bột gỗ ép, than chì là một khối trụ ở trung tâm có đường kính \(\frac{1}{4}\,{\rm{cm}}\), giá thành \(540\) đồng\(/{{\mathop{\rm cm}\nolimits} ^3}\). Bột gỗ ép xung quanh có giá thành \(100\) đồng\(/{{\mathop{\rm cm}\nolimits} ^3}\). Tính giá của một cái bút chì được công ty bán ra biết giá nguyên vật liệu chiếm \(15,58\,\% \) giá thành sản phẩm.
Một lọ thủy tinh dạng hình trụ có đựng sẵn một lượng nước có thể tích là \(V = 224,7456c{m^3}\). Người ta bỏ một khối lập phương \(ABC
D.A’B’C’D’\) vào lọ thủy tinh thì đỉnh A chạm đáy lọ (đáy thứ nhất của hình trụ) và các đỉnh \(A’,B,D\) nằm trên đường tròn miệng của lọ (đáy thứ hai của hình trụ) (xem hình vẽ). Biết rằng sau khi bỏ khối lập phương vào thì lượng nước dâng lên vừa đầy lọ thủy tinh và ta lấy các giá trị gần đúng sau đây \(\pi \approx 3,14\), \(\sqrt 3 \approx 1,73\), \(\sqrt 2 \approx 1,41\). Thể tích của khối lập phương là: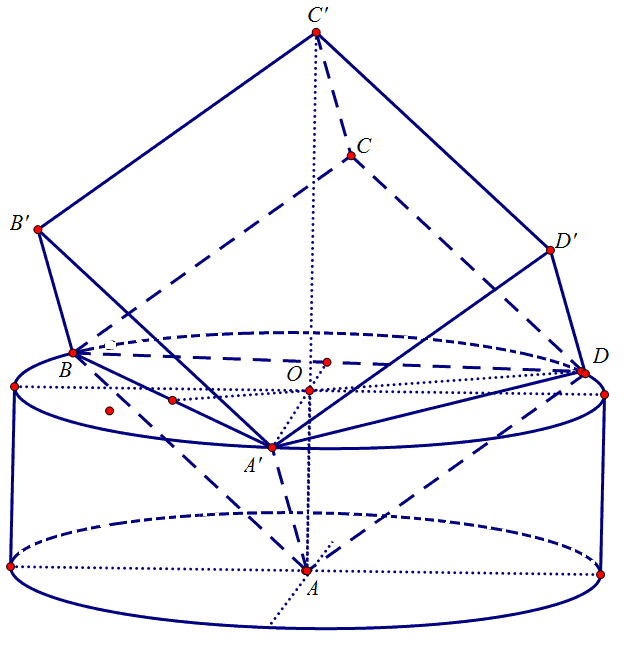
Câu hỏi:
Một lọ thủy tinh dạng hình trụ có đựng sẵn một lượng nước có thể tích là \(V = 224,7456c{m^3}\). Người ta bỏ một khối lập phương \(ABC
D.A'B'C'D'\) vào lọ thủy tinh thì đỉnh A chạm đáy lọ (đáy thứ nhất của hình trụ) và các đỉnh \(A',B,D\) nằm trên đường tròn miệng của lọ (đáy thứ hai của hình trụ) (xem hình vẽ). Biết rằng sau khi bỏ khối lập phương vào thì lượng … [Đọc thêm...] vềMột lọ thủy tinh dạng hình trụ có đựng sẵn một lượng nước có thể tích là \(V = 224,7456c{m^3}\). Người ta bỏ một khối lập phương \(ABC
D.A’B’C’D’\) vào lọ thủy tinh thì đỉnh A chạm đáy lọ (đáy thứ nhất của hình trụ) và các đỉnh \(A’,B,D\) nằm trên đường tròn miệng của lọ (đáy thứ hai của hình trụ) (xem hình vẽ). Biết rằng sau khi bỏ khối lập phương vào thì lượng nước dâng lên vừa đầy lọ thủy tinh và ta lấy các giá trị gần đúng sau đây \(\pi \approx 3,14\), \(\sqrt 3 \approx 1,73\), \(\sqrt 2 \approx 1,41\). Thể tích của khối lập phương là:
Từ độ cao \(63\left( m \right)\) của tháp nghiêng Pi-sa ở Italia, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được ngay trước đó. Tính độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất biết quả bóng chỉ rơi xuống và nảy lên theo chiều thẳng đứng.
Câu hỏi: Từ độ cao \(63\left( m \right)\) của tháp nghiêng Pi-sa ở Italia, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được ngay trước đó. Tính độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất biết quả bóng chỉ rơi xuống và nảy lên theo chiều … [Đọc thêm...] vềTừ độ cao \(63\left( m \right)\) của tháp nghiêng Pi-sa ở Italia, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được ngay trước đó. Tính độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất biết quả bóng chỉ rơi xuống và nảy lên theo chiều thẳng đứng.
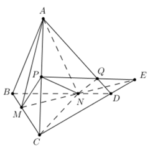
Cho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\)
Cho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\). Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) A. \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{26}}{{19}}\) … [Đọc thêm...] vềCho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\)