Tỷ số thể tích khối đa diện

Tỷ số thể tích khối đa diện

Công thức tỉ số thể tích của khối chóp tam giác:

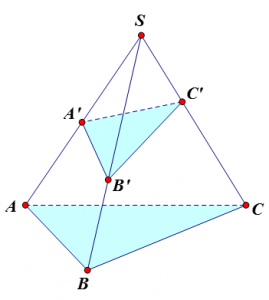
Trên các đường thẳng SA, SB, SC của hình chóp S.ABC ta lấy lần lượt các điểm A’, B’, C’. Ta có:

$\frac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \frac{{SA’}}{{SA}}.\frac{{SB’}}{{SB}}.\frac{{SC’}}{{SC}}.$

Ví dụ 1:

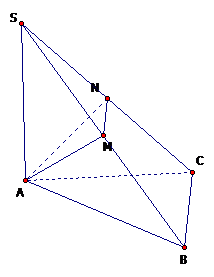
Cho hình chóp S.ABC có tam giác ABC đều cạnh 2a, cạnh bên SA vuông góc với mặt phẳng đáy và \(SA=a\sqrt3.\)Gọi M, N lần lượt là trung điểm của SB và SC. Tính thể tích khối chóp S.AMN và A.BCNM.

Lời giải:

Khối chóp S.AMN và S.ABC có chung đỉnh S và góc ở đỉnh S.

Do đó theo công thức tỷ số thể tích, ta có:

\(\frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{{\rm{SA}}}}{{{\rm{SA}}}}.\frac{{SM}}{{SB}}.\frac{{SN}}{{SC}} = 1.\frac{1}{2}.\frac{1}{2} = \frac{1}{4}\)

Suy ra: \({V_{S.AMN}} = \frac{{{V_{S.ABC}}}}{4} = \frac{{\frac{1}{3}.{a^2}\sqrt 3 .a\sqrt 3 }}{4} = \frac{{{a^3}}}{4}\)

Và: \({V_{A.BCNM}} = \frac{3}{4}.{V_{S.ABC}} = {\frac{{3a}}{4}^3}.\)

Ví dụ 2:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\).

Lời giải:

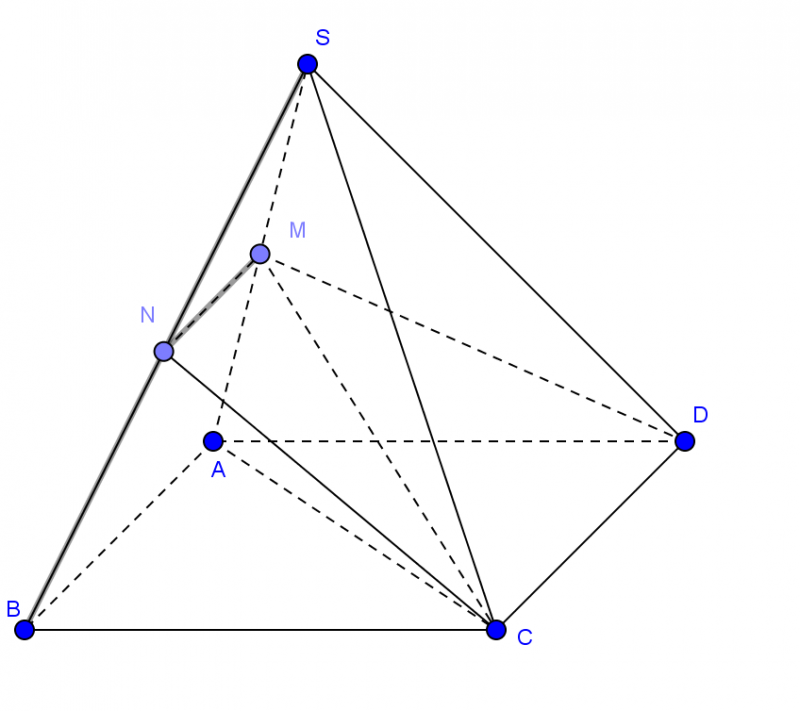
Ta có:

\({V_{S.MNCD}} = {V_{S.MCD}} + {V_{S.MNC}}\) và \({V_{S.ABCD}} = {V_{S.ACD}} + {V_{S.ABC}}\).

Khi đó: \(\frac{{{V_{S.MCD}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}} = \frac{1}{2} \Leftrightarrow {V_{S.MCD}} = \frac{1}{4}{V_{S.ABCD}}\)

Mặt khác: \(\frac{{{V_{S.MNC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}} = \frac{1}{4} \Rightarrow {V_{S.MNC}} = \frac{1}{8}{V_{S.ABCD}}\)

Từ trên suy ra \({V_{S.MNCD}} = \left( {\frac{1}{4} + \frac{1}{8}} \right){V_{S.ABCD}} = \frac{3}{8}{V_{S.ABCD}}\).

Ví dụ 3 : Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân ở $B$, $AC = a\sqrt 2 $, $SA$ vuông góc với đáy $ABC$, $SA = a.$
1. Tính thể tích của khối chóp $S.ABC.$
2. Gọi $G$ là trọng tâm tam giác $SBC$, mặt phẳng $(α)$ qua $AG$ và song song với $BC$ cắt $SC, SB$ lần lượt tại $M, N$. Tính thể tích của khối chóp $S.AMN.$

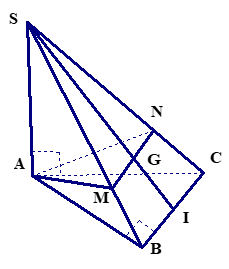
1. Ta có: $ΔABC$ vuông cân tại $B$ có $AC = a\sqrt 2 $, suy ra $AB = BC = a.$
${V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SA$ $ = \frac{1}{3}.\frac{1}{2}AB.BC.SA = \frac{{{a^3}}}{6}.$
2. Gọi $I$ là trung điểm $BC.$
Vì $G$ là trọng tâm tam giác $ΔSBC$ nên ta có: $\frac{{SG}}{{SI}} = \frac{2}{3}.$
Vì $(α) // BC$ nên $MN // BC$, do đó: $\frac{{SM}}{{SB}} = \frac{{SN}}{{SC}} = \frac{{SG}}{{SI}} = \frac{2}{3}.$
$ \Rightarrow \frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}}.\frac{{SM}}{{SB}}.\frac{{SN}}{{SC}} = \frac{4}{9}.$
Vậy ${V_{S.AMN}} = \frac{4}{9}.{V_{S.ABC}} = \frac{{2{a^3}}}{{27}}.$

Ví dụ 4 : Cho khối chóp tứ giác đều $S.ABCD$ có thể tích là $V_{0}$. Một mặt phẳng $(α)$ qua $A, B$ và trung điểm $M$ của $SC$ cắt $SD$ tại $N$. Tính thể tích khối chóp $S.ABMN$.

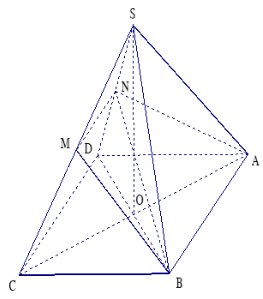
Dễ thấy $N$ là trung điểm của $SD.$
Ta có: $\frac{{{V_{S.ANB}}}}{{{V_{S.ADB}}}} = \frac{{SA}}{{SA}}.\frac{{SN}}{{SD}}.\frac{{SB}}{{SB}} = \frac{1}{2}$ $ \Rightarrow {V_{S.ANB}} = \frac{1}{2}.{V_{S.ADB}} = \frac{1}{4}.{V_{S.ABCD}}.$ $= \frac{1}{4}.{V_{0}}.$
Tương tự: ${V_{S.BMN}} = \frac{1}{4}.{V_{S.BCD}} = \frac{1}{8}.{V_0}.$
Do đó: ${V_{S.ABMN}} = {V_{S.ANB}} + {V_{S.BMN}} = \frac{3}{8}.{V_0}.$