Thể tích khối chóp

Thể tích khối chóp, Hình chóp

CÔNG THỨC

• Thể tích của 1 khối chóp bắng một phần ba tích số của mặt đáy và chiều cao khối chóp đó: \(V=\frac{1}{3}S_{day}.h.\)
• \(V=\frac{1}{3}B.h.\) trong đó B là diện tích đáy, h là chiều cao của khối chóp.

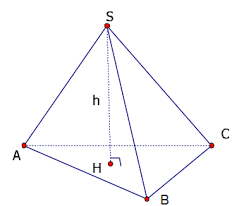
\(V_{S.ABCD}=\frac{1}{3}S_{ABC}.SH\)

Để tính thể tích khối chóp $S.{A_1}{A_2}…{A_n}$ ta đi tính đường cao và diện tích đáy. Khi xác định chân đường cao của hình chóp cần chú ý:
• Hình chóp đều thì chân của đường cao là tâm của đáy.
• Hình chóp có mặt bên $(S{A_i}{A_k})$ vuông góc với mặt đáy thì chân đường cao của tam giác $S{A_i}{A_k}$ hạ từ $S$ là chân đường cao của hình chóp.
• Nếu có hai mặt phẳng đi qua đỉnh và cùng vuông góc với đáy thì giao tuyến của hai mặt phẳng đó vuông góc với đáy.
• Nếu các cạnh bên của hình chóp bằng nhau thì hình chiếu của đỉnh là tâm đường tròn ngoại tiếp đáy.
• Nếu các mặt bên tạo với đáy một góc bằng nhau thì hình chiếu của đỉnh là tâm đường tròn nội tiếp đáy.

---

Dạng 1: Khối chóp có cạnh bên vuông góc với đáy

Ví dụ 1:

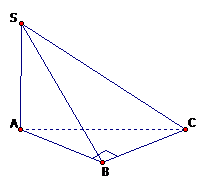
Cho hình chóp S.ABC có tam giác ABC vuông tại B, \(AB=a \sqrt 2, AC=a \sqrt 3\), cạnh bên SA vuông góc với mặt phẳng đáy và \(SB=a \sqrt 3.\) Tính thể tích khối chóp S.ABC.

Lời giải:

Tam giác ABC vuông tại B nên \(BC = \sqrt {A{C^2} – A{B^2}} = a.\)

Suy ra: \({{\rm{S}}_{\Delta {\rm{ABC}}}} = \frac{1}{2}BA.BC = \frac{1}{2}.a\sqrt 2 .a = \frac{{{a^2}.\sqrt 2 }}{2}\)

 

Tam giác SAB vuông tại A có \(SA = \sqrt {S{B^2} – A{B^2}} = a.\)

Vậy thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{{a^2}.\sqrt 2 }}{2}.a = \frac{{{a^3}.\sqrt 2 }}{6}.\)

Ví dụ 2:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt2\), cạnh bên SA vuông góc với mặt phẳng đáy và \(SC=a \sqrt5\). Tính thể tích khối chóp S.ABCD.

Lời giải:

 

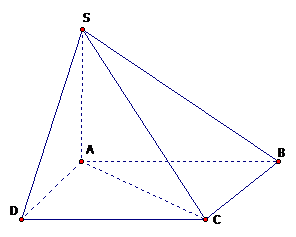
Diện tích ABCD: \({{\rm{S}}_{{\rm{ABCD}}}} = {\left( {a\sqrt 2 } \right)^2} = 2{a^2}.\)

Ta có: \(AC = AB.\sqrt 2 = a\sqrt 2 .\sqrt 2 = 2a.\)

Tam giác SAC vuông tại A nên: \(SA = \sqrt {S{C^2} – A{C^2}} = a\).

Vậy thể tích khối chóp S.ABCD là: \({V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SA = \frac{1}{3}.2{a^2}.a = \frac{{2{a^3}}}{3}.\)

Ví dụ 3 : Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$ với $AC = a$ biết $SA$ vuông góc với đáy $(ABC)$ và $SB$ hợp với đáy một góc $60°$.
1. Chứng minh các mặt bên là tam giác vuông.
2. Tính thể tích hình chóp.

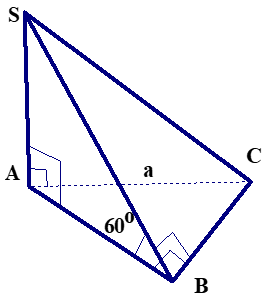
1. $SA \bot (ABC)$ $ \Rightarrow SA \bot AB$ và $SA \bot AC.$
Mà $BC \bot AB \Rightarrow BC \bot SB.$
Vậy các mặt bên của hình chóp là tam giác vuông.
2. Ta có $SA \bot (ABC)$ $ \Rightarrow AB$ là hình chiếu của $SB$ trên $(ABC).$
Do đó $\widehat {\left( {SB,\left( {ABC} \right)} \right) = }\widehat {SAB} = {60^o}.$
$\Delta ABC$ vuông cân nên $BA = BC = \frac{a}{{\sqrt 2 }}.$
${S_{ABC}} = \frac{1}{2}BA.BC = \frac{{{a^2}}}{4}.$
$\Delta SAB$ vuông tại $A$ nên $ \Rightarrow SA = AB.{\mathop{\rm t}\nolimits} a{\rm{n6}}{0^o} = \frac{{a\sqrt 6 }}{2}.$
Vậy: $V = \frac{1}{3}{S_{ABC}}.SA$ $ = \frac{1}{3}\frac{{{a^2}}}{4}\frac{{a\sqrt 6 }}{2} = \frac{{{a^3}\sqrt 6 }}{{24}}.$

Ví dụ 4:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt đáy một góc bằng 60⁰.Tính thể tích khối chóp S.ABCD.

Lời giải:

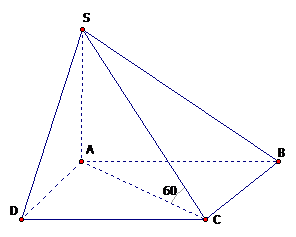
\(SA \bot (ABCD)\) nên AC là hình chiếu của SC lên mặt mặt phẳng (ABCD).

Do đó: \(\widehat {(SC,(ABCD))} = \widehat {(SC,AC)} = \widehat {SCA} = {60^o}.\)

Diện tích đáy là: \({{\rm{S}}_{{\rm{ABCD}}}} = {a^2}.\)

Tam giác SAC vuông tại A có \(AC=a \sqrt2, \widehat {SCA} = {60^0} \Rightarrow SA = AC.\tan {60^o} = a\sqrt 6.\)

Vậy thể tích khối chóp là: \({V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SA = \frac{1}{3}.{a^2}.a\sqrt 6 = \frac{{{a^3}.\sqrt 6 }}{3}.\)

Ví dụ 5:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh \(BC=a\sqrt2,\) cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45⁰ .Tính thể tích khối chóp S.ABC.

Lời giải:

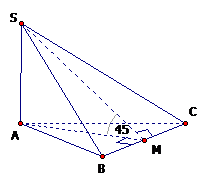
Gọi M là trung điểm của BC ta có: \(AM \bot BC\).

Mặt khác: \(SA \bot BC\) do \(SA \bot \left( {ABC} \right).\)

Nên: \(BC \bot (SAM) \Rightarrow SM \bot BC.\)

Suy ra: \(\widehat {((SBC),(ABC))} = \widehat {(SM,AM)} = \widehat {SMA} = {45^o}\).

Tam giác ABC vuông cận tại A có \(BC=a\sqrt2\) suy ra:

\(AB = BC = a\) và \(AM = \frac{{a\sqrt 2 }}{2}\) \(\Rightarrow {{\rm{S}}_{\Delta {\rm{ABC}}}} = \frac{1}{2}AB.AC = \frac{1}{2}.a.a = \frac{{{a^2}}}{2}\)

Tam giác SAM vuông tại A có \(AM = \frac{{a\sqrt 2 }}{2}\) và \(\widehat {SMA} = {45^o}\)

Suy ra: \(SA = AB.\tan {45^o} = \frac{{a\sqrt 2 }}{2}.\)

Vậy thể tích khối chóp S.ABC là:

\({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{{a^2}}}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}.\sqrt 2 }}{{12}}\).

---

Dạng 2: Khối chóp ĐỀU

Ví dụ 1:

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng \(a\sqrt3\), cạnh bên bằng 2a.Tính thể tích khối chóp S.ABC.

Lời giải:

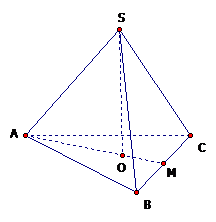
Gọi M là trung điểm của BC.

O là trọng tâm tam giác ABC suy ra \(SO \bot (ABC).\)

Tam giác ABC đều cạnh \(a\sqrt3\) suy ra:

\(AM=a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3a}}{2}.\)

\({\rm{AO = }}\frac{{\rm{2}}}{{\rm{3}}}.AM = \frac{2}{3}.\frac{{3a}}{2} = a\).

\({{\rm{S}}_{\Delta {\rm{ABC}}}} = \frac{1}{2}AB.AC.\sin {60^0} = \frac{1}{2}.a\sqrt 3 .a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3{a^2}.\sqrt 3 }}{4}\).

Tam giác SAO vuông tại A nên ta có \(SO = \sqrt {S{A^2} – A{O^2}} = a.\sqrt 3.\)

Vậy thể tích khối chóp S.ABC là:

\({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{3{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}.\sqrt 3 }}{4}.\)

Ví dụ 2 : Cho hình chóp tứ giác đều $S.ABCD$ có khoảng cách từ tâm $O$ của đáy đến mặt bên là $a$, góc giữa đường cao và mặt bên là ${30^0}.$ Tính thể tích của khối chóp $S.ABCD.$

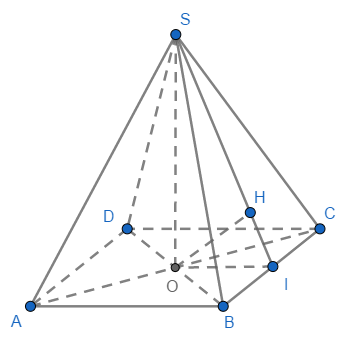
Gọi $I$ là trung điểm của cạnh $BC$, ta có $BC \bot \left( {SOI} \right)$ (do $BC \bot OI, BC \bot SO$), suy ra $\left( {SBC} \right) \bot \left( {SOI} \right).$
Dựng $OH \bot SI \left( {S \in I} \right)$ thì $OH \bot \left( {SBC} \right)$ và hình chiếu vuông góc của đường thẳng $SO$ lên mặt phẳng $\left( {SBC} \right)$ là đường thẳng $SI$, do đó $OH = d\left( {O,\left( {SBC} \right)} \right) = a$ và $\left( {SO,\left( {SBC} \right)} \right) = \widehat {OSI} = {30^0}$ (theo giả thiết).
Trong tam giác vuông $SOE$: $SO = \frac{{OH}}{{{\mathop{\rm s}\nolimits} {\rm{in3}}{0^0}}} = 2a$, $OI = SO\tan {30^0} = \frac{{2a\sqrt 3 }}{3}.$
Suy ra $AB = 2OI = \frac{{4a\sqrt 3 }}{3}.$
Thể tích của khối chóp $S.ABCD$: $V = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}A{B^2}.SO$ $ = \frac{1}{3}{\left( {\frac{{4a\sqrt 3 }}{3}} \right)^2}.2a = \frac{{32{a^3}}}{9}.$

---

Dạng 3: Khối chóp có MẶT bên vuông góc với đáy

Ví dụ 1 : Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông có cạnh $a.$ Mặt bên $SAB$ là tam giác đều nằm trong mặt phẳng vuông góc với đáy $(ABCD).$
1. Chứng minh rằng chân đường cao khối chóp trùng với trung điểm cạnh $AB.$
2. Tính thể tích khối chóp $S.ABCD.$

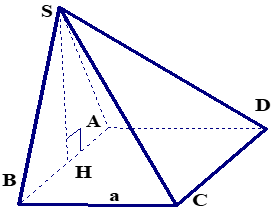
1. Gọi $H$ là trung điểm của $AB.$
$\Delta SAB$ đều $ \Rightarrow SH \bot AB.$
Mà $(SAB) \bot (ABCD) \Rightarrow SH \bot (ABCD).$
Do đó $H$ là chân đường cao của khối chóp.
2. Ta có tam giác $SAB$ đều nên $SH = \frac{{a\sqrt 3 }}{2}.$
Suy ra $V = \frac{1}{3}{S_{ABCD}}.SH = \frac{{{a^3}\sqrt 3 }}{6}.$

Ví dụ 2 : Cho tứ diện $ABCD$ có $ABC$ là tam giác đều, $BCD$ là tam giác vuông cân tại $D$, $(ABC) ⊥ (BCD)$ và $AD$ hợp với $(BCD)$ một góc $60°$. Tính thể tích tứ diện $ABCD.$

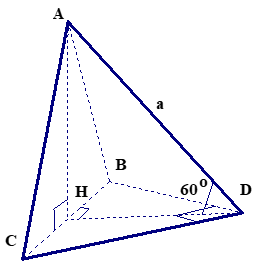
Gọi $H$ là trung điểm của $BC.$
Ta có tam giác $ABC$ đều nên $AH \bot BC.$
Mà $(ABC) ⊥ (BCD)$ nên $AH \bot (BCD).$
Ta có $ΔAHD$ vuông tại $H$ nên $AH = AD.tan{60^o} = a\sqrt 3 $ và $HD = AD.cot{60^o} = \frac{{a\sqrt 3 }}{3}.$
$\Delta BCD$ vuông tại $D$ nên $BC = 2HD = \frac{{2a\sqrt 3 }}{3}.$
Vậy $V = \frac{1}{3}{S_{BCD}}.AH$ $ = \frac{1}{3}.\frac{1}{2}BC.HD.AH = \frac{{{a^3}\sqrt 3 }}{9}.$

Ví dụ 3 : Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, tam giác $SAB$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng $(SAC)$ và $(SCD)$ tạo với đáy lần lượt các góc ${60^0}$ và ${30^0}.$ Tính thể tích khối chóp $S.ABCD.$

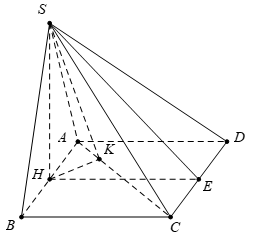
Gọi $H$ là trung điểm của $AB$ $\Rightarrow SH \bot AB.$
Mà $(SAB) \bot (ABCD)$ $ \Rightarrow SH \bot (ABCD)$ $ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SH.{S_{ABCD}}.$
Vẽ $HK \bot AC$ $ \Rightarrow AC \bot (SHK)$ $ \Rightarrow \widehat {SKH}$ là góc giữa hai mặt phẳng $(SAC)$ và mặt đáy nên $\widehat {SKH} = {60^0}.$
Vẽ $HE \bot CD$ $ \Rightarrow CD \bot (SHE)$ $ \Rightarrow \widehat {SEH}$ là góc giữa hai mặt phẳng $\left( {SCD} \right)$ và mặt đáy nên $\widehat {SEH} = {30^0}.$
Đặt $AB = x$, trong tam giác $SHE$ ta có: $SH = HE.\tan {30^0} = \frac{{x\sqrt 3 }}{3}$ $(1).$
Ta có $\Delta AKH \sim \Delta ABC$ $ \Rightarrow \frac{{KH}}{{BC}} = \frac{{AH}}{{AC}}$ $ \Rightarrow KH = \frac{{ax}}{{2\sqrt {{a^2} + {x^2}} }}.$
Trong tam giác $SHK$ ta có: $SH = HK\tan {60^0}$ $ = \frac{{ax\sqrt 3 }}{{2\sqrt {{a^2} + {x^2}} }}$ $(2).$
Từ $(1)$ và $(2)$, suy ra: $\frac{{x\sqrt 3 }}{3} = \frac{{ax\sqrt 3 }}{{2\sqrt {{a^2} + {x^2}} }}$ $ \Leftrightarrow \sqrt {{x^2} + {a^2}} = \frac{{3a}}{2}$ $ \Rightarrow x = \frac{{a\sqrt 5 }}{2}.$
Vậy thể tích khối chóp $S.ABCD$ là: $V = \frac{1}{3}SH.AB.AD$ $ = \frac{1}{3}.\frac{{x\sqrt 3 }}{3}.a.x = \frac{{5{a^3}\sqrt 3 }}{{36}}.$