Lý thuyết thể tích của khối đa diện

1. Tính chất của thể tích khối đa diện

• Hai khối đa diện bằng nhau thì có thể tích bằng nhau.
• Nếu 1 khối đa diện được phân chia thành các khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ.
• Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1.

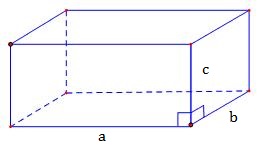
2. Thể tích khối hộp chữ nhật

Giả sử có 1 khối hộp chữ nhật với 3 kích thước a, b, c đều là những số dương. Khi đó thể tích của nó là: \(V=a.b.c\).

Thể tích khối lập phương cạnh a. $V=a^3$

3. Thể tích khối chóp

• Thể tích của 1 khối chóp bắng một phần ba tích số của mặt đáy và chiều cao khối chóp đó: \(V=\frac{1}{3}S_{day}.h.\)
• \(V=\frac{1}{3}B.h.\) trong đó B là diện tích đáy, h là chiều cao của khối chóp.

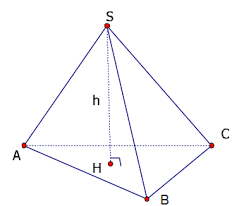
\(V_{S.ABCD}=\frac{1}{3}S_{ABC}.SH\)

Để tính thể tích khối chóp $S.{A_1}{A_2}…{A_n}$ ta đi tính đường cao và diện tích đáy. Khi xác định chân đường cao của hình chóp cần chú ý:
• Hình chóp đều thì chân của đường cao là tâm của đáy.
• Hình chóp có mặt bên $(S{A_i}{A_k})$ vuông góc với mặt đáy thì chân đường cao của tam giác $S{A_i}{A_k}$ hạ từ $S$ là chân đường cao của hình chóp.
• Nếu có hai mặt phẳng đi qua đỉnh và cùng vuông góc với đáy thì giao tuyến của hai mặt phẳng đó vuông góc với đáy.
• Nếu các cạnh bên của hình chóp bằng nhau thì hình chiếu của đỉnh là tâm đường tròn ngoại tiếp đáy.
• Nếu các mặt bên tạo với đáy một góc bằng nhau thì hình chiếu của đỉnh là tâm đường tròn nội tiếp đáy.

Công thức tỉ số thể tích của khối chóp tam giác:

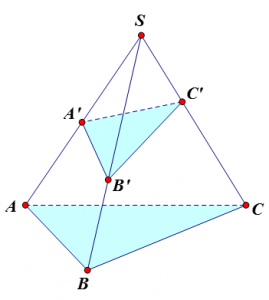
Trên các đường thẳng SA, SB, SC của hình chóp S.ABC ta lấy lần lượt các điểm A’, B’, C’. Ta có:

$\frac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \frac{{SA’}}{{SA}}.\frac{{SB’}}{{SB}}.\frac{{SC’}}{{SC}}.$

4. Thể tích khối lăng trụ

Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy với chiều cao của khối lăng trụ đó:

\(V=B.h.\) (trong đó B là diện tích đáy, h là chiều cao của khối lăng trụ)

\(V=S_{day}.h.\)

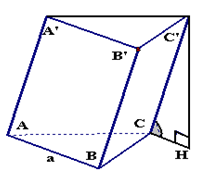
\(V_{ABC.A’B’C’}=S_{ABC}.C’H\)

Để tính thể tích của khối lăng trụ ta cần đi tính chiều cao của lăng trụ và diện tích đáy.

Các tính chất của lăng trụ :
a. Hình lăng trụ
• Các cạnh bên của hình lăng trụ song song và bằng nhau.
• Các mặt bên của hình lăng trụ là các hình bình hành.
• Hai đáy của hình lăng trụ là hai đa giác bằng nhau và nằm trong hai mặt phẳng song song với nhau.
• Lăng trụ có các cạnh bên vuông góc hai đáy được gọi là lăng trụ đứng.
* Các cạnh bên của lăng trụ đứng chính là đường cao của nó.
* Các mặt bên của lăng trụ đứng là các hình chữ nhật.
• Lăng trụ đứng có đáy là đa giác đều được gọi là lăng trụ đều. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau.
b. Hình hộp: Là hình lăng trụ có đáy là hình bình hành:
• Hình hộp đứng có các cạnh bên vuông góc với đáy.
• Hình hộp đứng có đáy là hình chữ nhật được gọi là hình hộp chữ nhật.
• Hình hộp chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương.
• Đường chéo của hình hộp chữ nhật có ba kích thước $a, b, c$ là: $d = \sqrt {a^2 + b^2 + c^2}.$
• Đường chéo của hình lập phương cạnh $a$ là $d = a \sqrt 3.$