Công thức tính thể tích của 5 khối đa diện đều gồm tứ diện đều, khối lập phương, bát diện đều, khối 12 mặt đều và khối 20 mặt đều
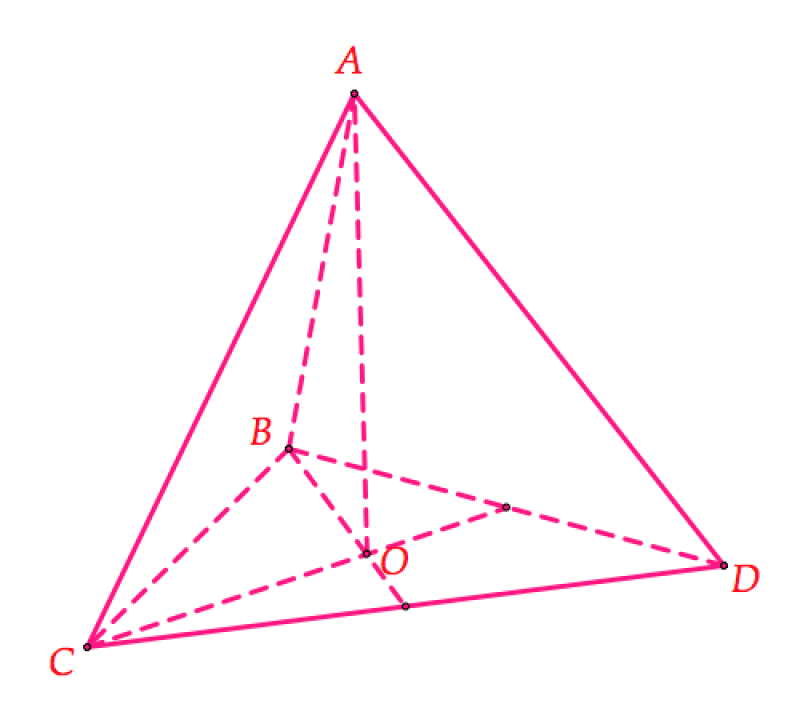
1. Tứ diện $ABCD$ đều cạnh $a,$
Ta có $S=\frac{{{a}^{2}}\sqrt{3}}{4}$ và $h=AO=\sqrt{A{{B}^{2}}-O{{B}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \frac{2}{3}.\frac{a\sqrt{3}}{2} \right)}^{2}}}=\frac{a\sqrt{6}}{3}.$
Do đó $V=\frac{1}{3}Sh=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}=\frac{{{a}^{3}}\sqrt{2}}{12}.$

2. Hình lập phương cạnh $a$.
Khối lập phương có thể tích $V=a^3$.
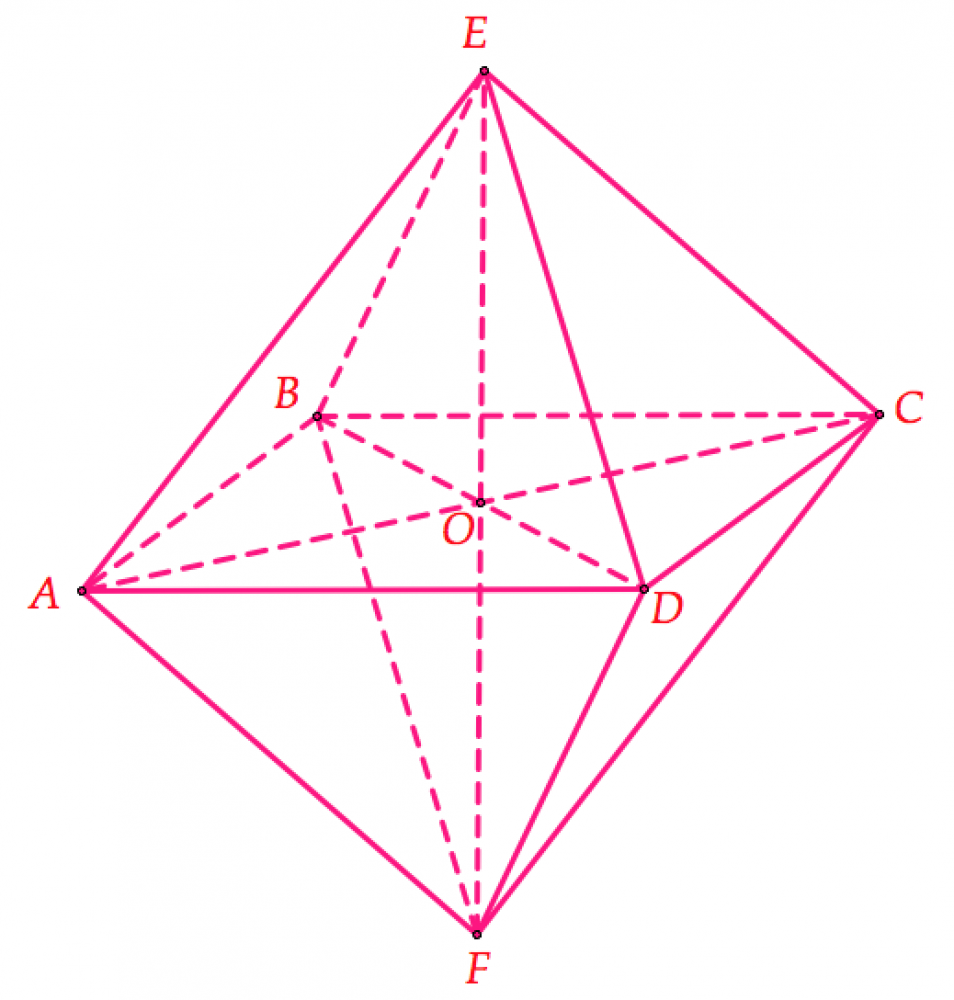
3. Khối bát diện đều $ABCDEF$ cạnh $a$, ta có
${{S}_{ABCD}}={{a}^{2}}$ và $EF=2EO=2\sqrt{B{{E}^{2}}-B{{O}^{2}}}=2\sqrt{{{a}^{2}}-{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}}=a\sqrt{2}.$
Do đó $V=\frac{1}{3}{{S}_{ABCD}}.EF=\frac{1}{3}.{{a}^{2}}.a\sqrt{2}=\frac{{{a}^{3}}\sqrt{2}}{3}.$
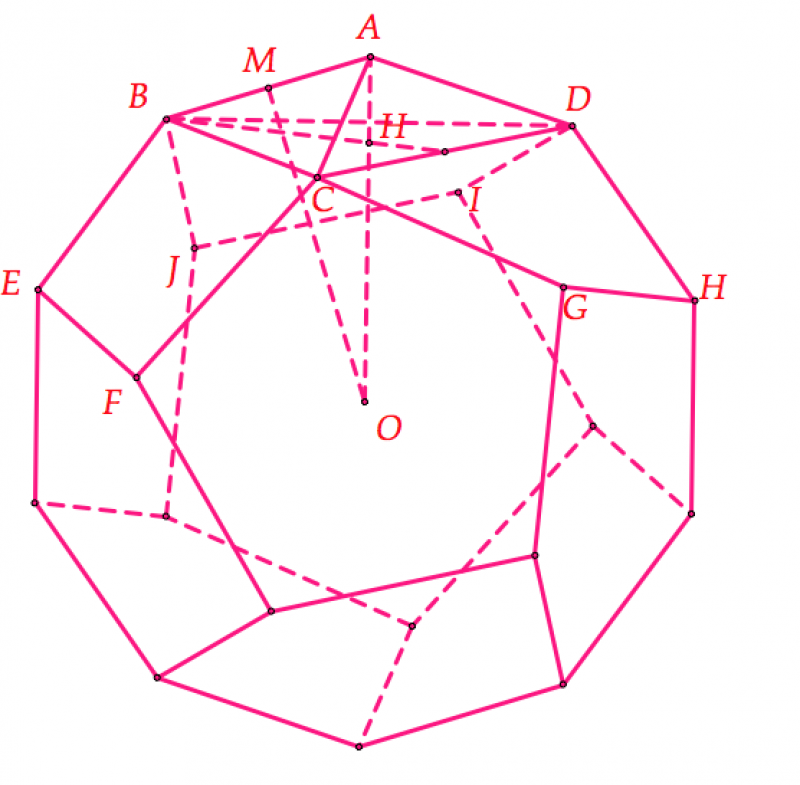
4. Khối 12 mặt đều cạnh $a$
Gọi $O$ là tâm mặt cầu ngoại tiếp đa diện 12 mặt đều, xét 3 mặt phẳng chung đỉnh $A$ là $ABEFC,ACGHD,ABJID.$
Khi đó $A.BCD$ là chóp tam giác đều và $OA$ vuông góc với mặt phẳng $(BCD)$ tại tâm ngoại tiếp $H$ của tam giác $BCD.$ Theo định lí hàm số côsin ta có
\[BC=CD=BD=\sqrt{{{a}^{2}}+{{a}^{2}}-2a.a.\cos \left( \dfrac{3\pi }{5} \right)}=\dfrac{1+\sqrt{5}}{2}a.\]
Do đó $AH=\sqrt{A{{B}^{2}}-{{\left( \dfrac{2}{3}.\dfrac{BC\sqrt{3}}{2} \right)}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \dfrac{1+\sqrt{5}}{2\sqrt{3}}a \right)}^{2}}}=\dfrac{\sqrt{5}-1}{2\sqrt{3}}a.$
Gọi $M$ là trung điểm cạnh $AB,$ ta có hai tam giác vuông $AHB\backsim AMO,$ do đó $\frac{AO}{AB}=\frac{AM}{AH}\Rightarrow R=AO=\frac{A{{B}^{2}}}{2AH}=\frac{{{a}^{2}}}{2.\frac{\sqrt{5}-1}{2\sqrt{3}}a}=\dfrac{a\sqrt{3}}{\sqrt{5}-1}.$
Ta có thể tích khối đa diện 12 mặt đều bằng tổng thể tích của 12 khối chóp ngũ giác đều cạnh đáy bằng $a,$ cạnh bên bằng $R=\dfrac{a\sqrt{3}}{\sqrt{5}-1}.$
Từ đó dễ có $V=\dfrac{{{a}^{3}}(15+7\sqrt{5})}{4}.$
*Chú ý. Có thể tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện đã cho (cũng chính là bán kính mặt cầu ngoại tiếp hình chóp $A.BCD$) bằng cách áp dụng công thức \[R=OA=\frac{A{{B}^{2}}}{2\sqrt{A{{B}^{2}}-R_{BCD}^{2}}}.\]
5. Khối đa diện đều 20 mặt đều cạnh $a,$ bằng cách thực hiện tương tự như khối đa diện 12 mặt đều ta có công thức xác định thể tích là $V=\dfrac{5(3+\sqrt{5}){{a}^{3}}}{12}.$
*Chú ý. Khối 12 mặt đều, khối 20 mặt đều chỉ để tham khảo; các bạn không nên chú ý nhiều .
