Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
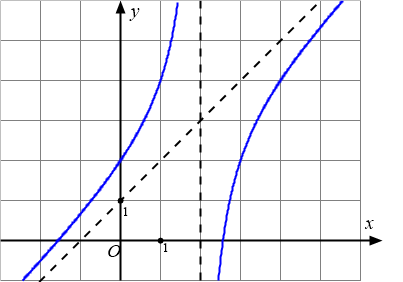
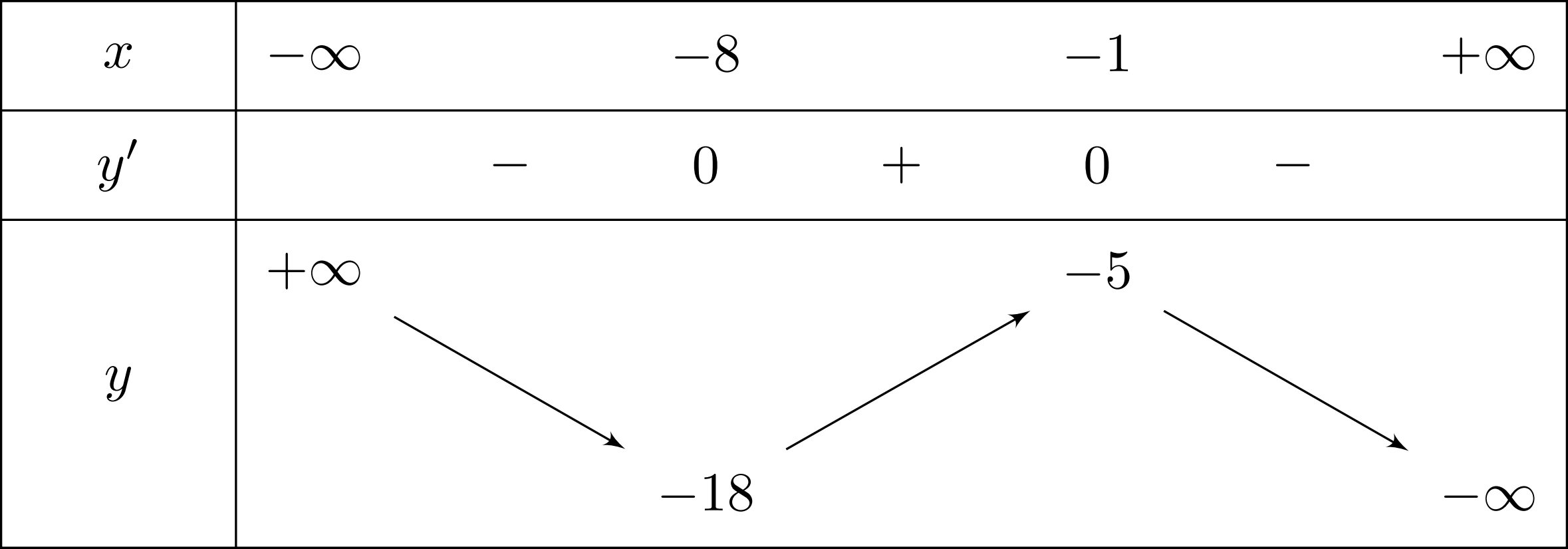
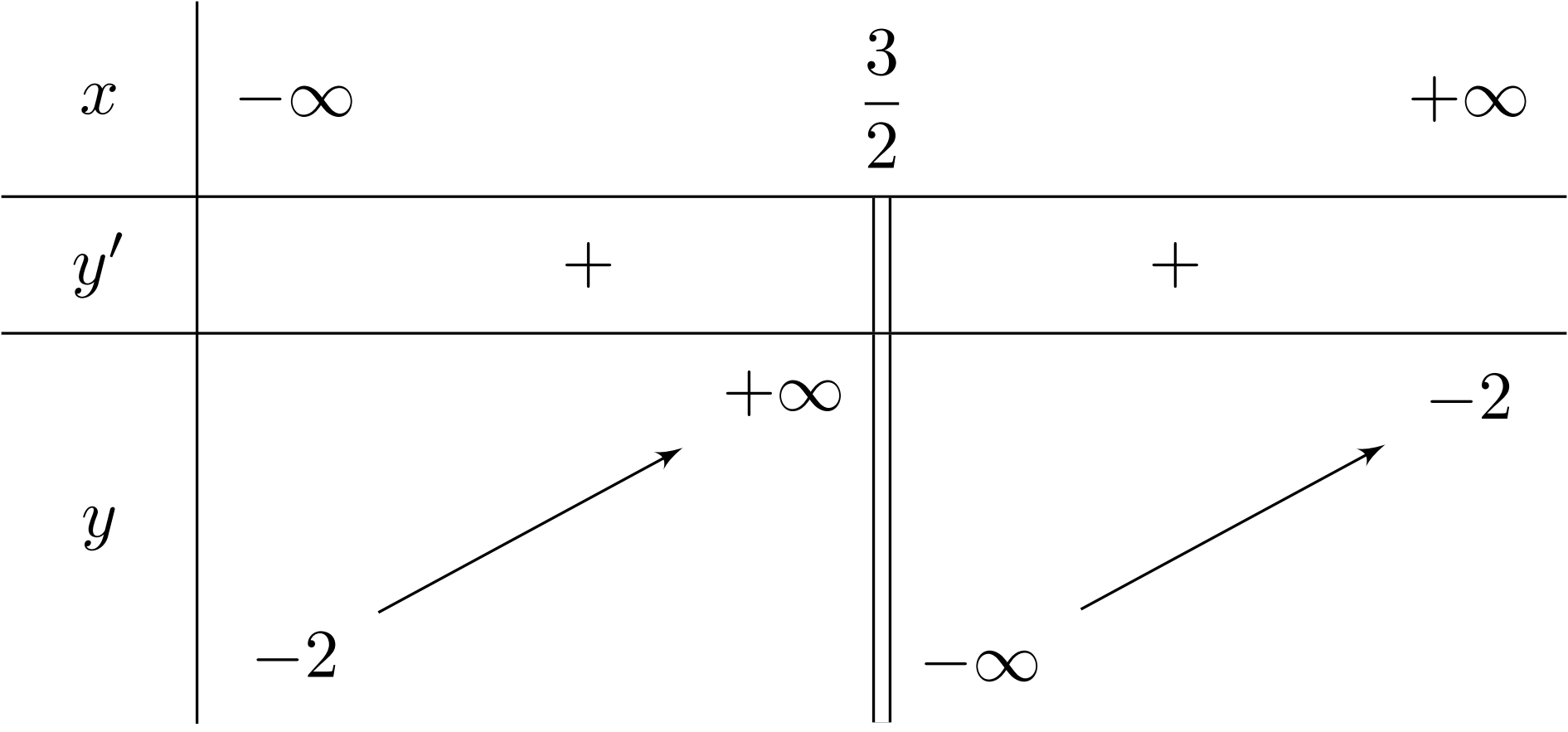
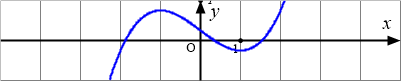
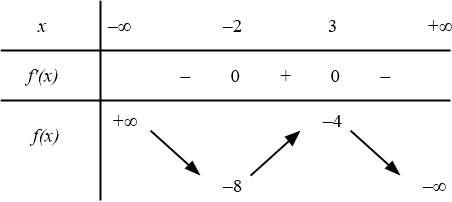
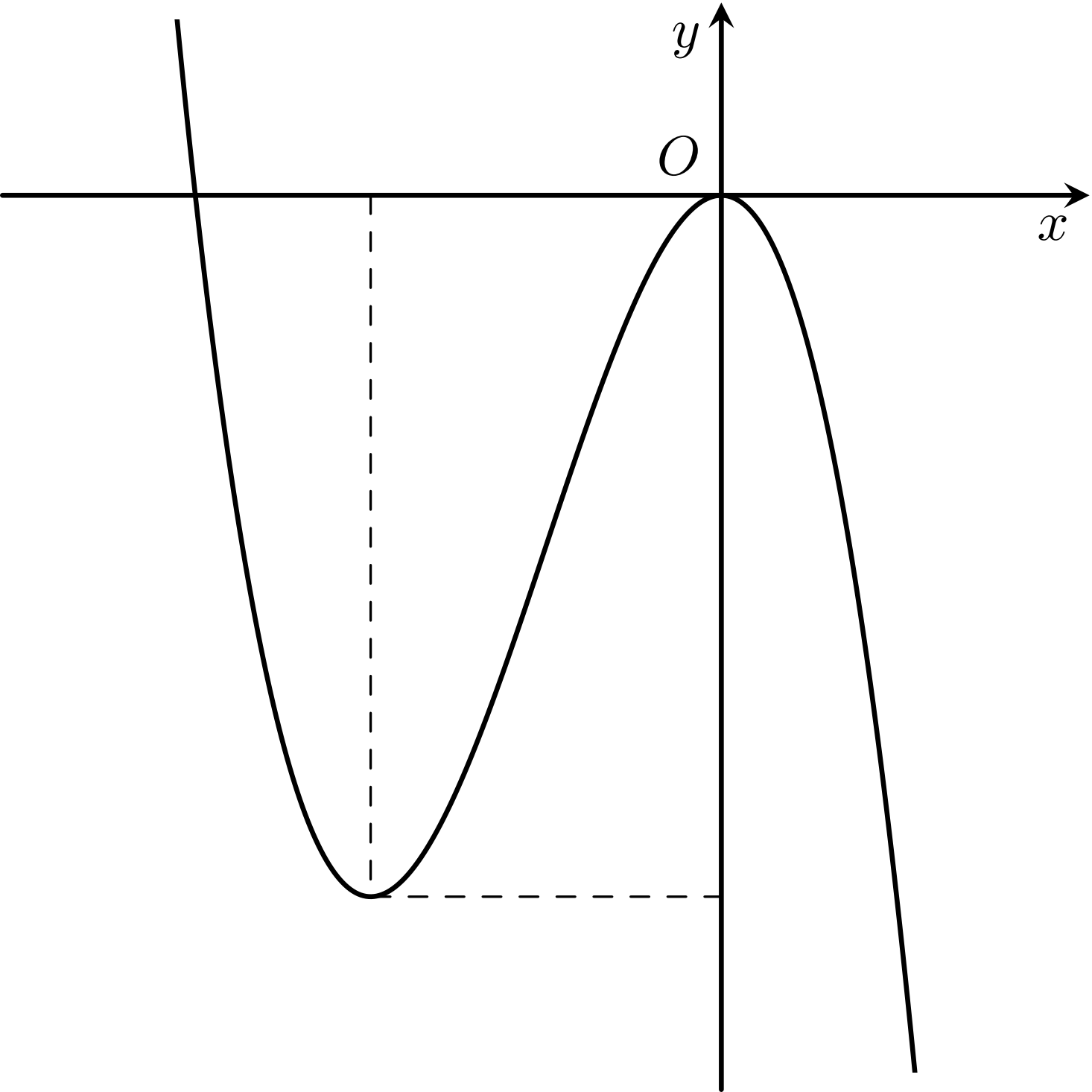
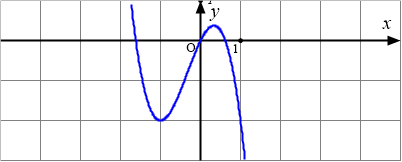
Bài toán gốc Đồ thị dưới đây là của hàm số nào?A. $y=\dfrac{x^2-2x+1}{x}$.B. $y=\dfrac{x^2-x-4}{x-2}$.C. $y=\dfrac{x^2+3x-3}{x+1}$.D. $y=\dfrac{x^2}{-x+1}$.Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.Còn lại hai hàm Phân thức bậc hai chia bậc hai có cùng tiệm cận đứng và tiệm cận … [Đọc thêm...] vềĐồ thị dưới đây là của hàm số nào?
Khẳng định nào dưới đây đúng?
Bài toán gốc Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có bảng biến thiên như sauKhẳng định nào dưới đây đúng?A. $a{<}0, b{<}0, c{>}0, d{<}0$.B. $a{<}0, b{<}0, c{<}0, d{<}0$.C. $a{<}0, b{>}0, c{>}0, d{>}0$.D. $a{<}0, b{>}0, c{<}0, d{<}0$.Lời giải: Từ bảng biến thiên ta thấyHàm số nghịch biến trên khoảng … [Đọc thêm...] vềCho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có bảng biến thiên như sau
Khẳng định nào dưới đây đúng?
Bài toán gốc Hàm số nào dưới đây có bảng biến thiên như sau?A. $y = \dfrac{-4x-3}{2x-1}$.B. $y = \dfrac{2x-3}{-4x-1}$.C. $y = \dfrac{2x-1}{-4x-3}$.D. $y = \dfrac{-4x-1}{2x-3}$.Lời giải: Dựa vào bảng biến thiên ta có$\bullet$ Đạo hàm $y^{\prime} {>} 0 \forall x \neq \dfrac{3}{2}$;$\bullet$ Đồ thị hàm số có tiệm cận đứng là $x = \dfrac{3}{2}$;$\bullet$ Đồ thị hàm … [Đọc thêm...] vềHàm số nào dưới đây có bảng biến thiên như sau?
Chọn phát biểu đúng?
Bài toán gốc Cho hàm số $y=f(x)=ax^3+bx^2+cx+d,a\neq 0$ có đồ thị như hình dưới đây:Chọn phát biểu đúng?A. $a{>}0,d{>}0$.B. $a{<}0,d{<}0$.C. $a{<}0,d{>}0$.D. $a{>}0,d{<}0$. Phân tích và Phương pháp giải Dạng toán nhận biết dấu các hệ số $a, b, c, d$ của hàm đa thức bậc ba $y=ax^3+bx^2+cx+d$ dựa vào đồ thị hàm số.1. Dấu … [Đọc thêm...] vềCho hàm số $y=f(x)=ax^3+bx^2+cx+d,a\neq 0$ có đồ thị như hình dưới đây:
Chọn phát biểu đúng?
Số giá trị nguyên $m$ để phương trình $f(x)=m+5$ có 3 nghiệm?
Bài toán gốc Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:Số giá trị nguyên $m$ để phương trình $f(x)=m+5$ có 3 nghiệm?A. $5$.B. $0$.C. $4$.D. $3$. Phân tích và Phương pháp giải Dạng bài toán là xét sự tương giao giữa đồ thị hàm số $y=f(x)$ và đường thẳng ngang $y=k$ (trong đó $k$ là biểu thức chứa tham số $m$), dựa trên bảng biến … [Đọc thêm...] vềCho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:
Số giá trị nguyên $m$ để phương trình $f(x)=m+5$ có 3 nghiệm?
Số lượng sản phẩm của công ty bán được trong $x$ (tháng) được tính bởi công thức $S\left( x \right)=300\left( 2+\frac{4}{x+2} \right)$ với $x\ge 1$. Xem $y=S\left( x \right)$ là một hàm số xác định trên $\left[ 1;+\infty \right)$. Khi đó, hãy tính xem số lượng sản phẩm của công ty bán được trong thời gian dài không thể thấp hơn bao nhiêu sản phẩm?Lời giảiTrả lời: 600Ta có: … [Đọc thêm...] vềSố lượng sản phẩm của công ty bán được trong $x$ (tháng) được tính bởi công thức $S\left( x \right)=300\left( 2+\frac{4}{x+2} \right)$ với $x\ge 1$
Số lượng sản phẩm của công ty bán được trong ${x}$ (tháng) được tính theo công thức ${S(x)=400\left(2+\frac{3}{x+2}\right)}$ với ${x \geq 1}$. Ta coi ${y=S(x)}$ là một hàm số xác định trên ${[1 ;+\infty)}$. Khi đó, hãy tính xem số lượng sản phẩm của công ty bán được trong một khoảng thời gian dài không thể thấp hơn bao nhiêu sản phẩm?Lời giảiTa có: … [Đọc thêm...] vềSố lượng sản phẩm của công ty bán được trong ${x}$ (tháng) được tính theo công thức ${S(x)=400\left(2+\frac{3}{x+2}\right)}$ với ${x \geq 1}$
$S\left( x \right)=200\left( 5-\frac{9}{2+x} \right)$, trong đó $x\ge 1$
Số lượng sản phẩm bán được của một công ty trong $x$ (tháng) được tính theo công thức$S\left( x \right)=200\left( 5-\frac{9}{2+x} \right)$, trong đó $x\ge 1$.Số lượng sản phẩm lớn nhất mà công ty có thể bán được trong $x$tháng là?Lời giảiĐáp án: 1000Số lượng sản phẩm bán được lớn nhất của công ty là tiệm cận ngang của hàm số $S\left( x \right)$.Tìm tiệm cận ngang của đồ thị hàm … [Đọc thêm...] vềSố lượng sản phẩm bán được của một công ty trong $x$ (tháng) được tính theo công thức $S\left( x \right)=200\left( 5-\frac{9}{2+x} \right)$, trong đó $x\ge 1$
Bài toán gốc Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?A. $a{<}0, b{>}0, c=0, d=0$.B. $a{<}0, b=0, c=0, d=0$.C. $a{<}0, b{<}0, c=0, d=0$.D. $a{<}0, b{<}0, c=0, d{>}0$.Lời giải: Từ hình vẽ ta thấyNhánh ngoài cùng bên phải, từ trái sang phải đi xuống nên $a{<}0$.Đồ thị cắt … [Đọc thêm...] vềCho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
Bài toán gốc Đồ thị của hàm số nào dưới đây có dạng như đường cong?A. $y=\dfrac{-x+5}{5x+3}$.B. $y=-2x^3-2x^2+2x$.C. $y=-3x^4+3x^2-2$.D. $y=-x^2+6x-3$. Phân tích và Phương pháp giải Dạng bài toán là nhận dạng đồ thị hàm số. Phương pháp giải dựa trên việc xác định các đặc điểm cơ bản của đồ thị:1. Loại hàm số: Xác định đồ thị thuộc loại hàm bậc … [Đọc thêm...] vềĐồ thị của hàm số nào dưới đây có dạng như đường cong?