Đồ thị của hàm số nào dưới đây có dạng như đường cong?

Bài toán gốc

Đồ thị của hàm số nào dưới đây có dạng như đường cong?

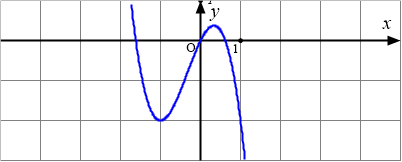
A. $y=\dfrac{-x+5}{5x+3}$.B. $y=-2x^3-2x^2+2x$.

C. $y=-3x^4+3x^2-2$.D. $y=-x^2+6x-3$.

Phân tích và Phương pháp giải

Dạng bài toán là nhận dạng đồ thị hàm số. Phương pháp giải dựa trên việc xác định các đặc điểm cơ bản của đồ thị:

1. Loại hàm số: Xác định đồ thị thuộc loại hàm bậc ba ($y=ax^3+…$), hàm trùng phương ($y=ax^4+bx^2+c$), hay hàm phân thức ($y=(ax+b)/(cx+d)$) dựa trên hình dạng, số điểm cực trị và sự tồn tại của tiệm cận.

2. Dấu của hệ số bậc cao nhất ($a$): Quan sát nhánh cuối cùng của đồ thị (khi $x \to +\infty$). Nếu đồ thị đi lên ($a>0$), đi xuống ($a<0$).

3. Số điểm cực trị: Hàm bậc ba có tối đa 2 cực trị; Hàm trùng phương có tối đa 3 cực trị (nếu $ab<0$); Hàm phân thức không có cực trị.

(Giả sử đồ thị trong bài toán gốc có dạng chữ ‘M’ (3 cực trị, nhánh cuối cùng đi xuống), thì nó là hàm trùng phương với $a<0$, phù hợp với đáp án C: $y=-3x^4+3x^2-2$.)

Bài toán tương tự

5 bài toán tương tự:

**Câu 1.** Đồ thị hàm số nào dưới đây có dạng như đường cong (Hình minh họa: Đồ thị hàm bậc ba, nhánh cuối cùng đi lên, có 2 cực trị)?

A. $y=x^3 – 6x^2 + 1$.

B. $y=-x^3 + 3x – 1$.

C. $y=\dfrac{2x+1}{x-3}$.

D. $y=x^4 – 2x^2 + 1$.

Đáp án đúng: A.

Giải thích: Đồ thị là hàm bậc ba ($y=ax^3+…$) có nhánh cuối cùng đi lên ($a>0$) và có 2 cực trị. Chỉ có A thỏa mãn ($a=1>0$).

**Câu 2.** Đường cong trong hình bên là đồ thị của một trong bốn hàm số sau. Đó là hàm số nào? (Hình minh họa: Đồ thị hàm trùng phương có dạng chữ ‘W’, hai nhánh ngoài cùng đi lên và có 3 điểm cực trị).

A. $y=-x^4 + 2x^2$.

B. $y=x^4 – 4x^2 – 1$.

C. $y=x^3 – 3x + 2$.

D. $y=\dfrac{2x-1}{x+3}$.

Đáp án đúng: B.

Giải thích: Đồ thị chữ ‘W’ là của hàm trùng phương $y=ax^4+bx^2+c$ với $a>0$ và có 3 cực trị (do $a$ và $b$ trái dấu). Chỉ có B thỏa mãn ($a=1>0$).

**Câu 3.** Cho đồ thị hàm số có hai đường tiệm cận là $x=1$ và $y=3$. Đây là đồ thị của hàm số nào?

A. $y=x^4 – 2x^2 + 1$.

B. $y=x^3 + 3x$.

C. $y=\dfrac{3x+2}{x-1}$.

D. $y=\dfrac{x+3}{2x+1}$.

Đáp án đúng: C.

Giải thích: Hàm số $y=\dfrac{ax+b}{cx+d}$ có TCĐ $x=-d/c$ và TCN $y=a/c$. Với $y=\dfrac{3x+2}{x-1}$, ta có $TCĐ: x=1$ và $TCN: y=3/1=3$.

**Câu 4.** Đồ thị hàm số nào dưới đây có dạng như đường cong (Hình minh họa: Đồ thị hàm bậc ba, nhánh cuối cùng đi xuống, có 2 cực trị)?

A. $y=2x^3 – 3x^2$.

B. $y=-2x^3 + 3x + 1$.

C. $y=2x^4 – 4x^2$.

D. $y=\dfrac{3x+1}{x-2}$.

Đáp án đúng: B.

Giải thích: Đồ thị là hàm bậc ba ($y=ax^3+…$) có nhánh cuối cùng đi xuống ($a<0$) và có 2 cực trị. Chỉ có B thỏa mãn ($a=-2<0$).

**Câu 5.** Đường cong trong hình bên là đồ thị của một trong bốn hàm số sau. Hàm số đó là? (Hình minh họa: Đồ thị hàm trùng phương có dạng chữ ‘M’, hai nhánh ngoài cùng đi xuống và có 3 điểm cực trị).

A. $y=3x^4 – 6x^2 + 1$.

B. $y=-x^4 + 2x^2 + 5$.

C. $y=x^3 – 3x + 3$.

D. $y=-x^3 + 3x^2 + 3$.

Đáp án đúng: B.

Giải thích: Đồ thị có dạng chữ ‘M’ là của hàm trùng phương $y=ax^4+bx^2+c$ với $a<0$ và có 3 cực trị (do $ab<0$). Chỉ có B thỏa mãn ($a=-1<0$ và $y’=-4x^3+4x=0$ có 3 nghiệm).