Cho hàm số $y=f(x)={{x}^{4}}-2{{x}^{2}}-5$. Các khẳng định sau là đúng hay sai ?

Bài toán gốc

Cho hàm số $y=f(x)={{x}^{4}}-2{{x}^{2}}-5$. Các khẳng định sau là đúng hay sai ?

a) Hàm số có 3 điểm cực trị.

b) Hàm số đồng biến trên $\left( 0;+\infty \right)$.

c) Điểm $M\left( 0;1 \right)$ là điểm cực tiểu của đồ thị hàm số $y=f(x)$.

d) Hàm số $y=f(x)$ và $y=f(2x)$ có cùng điểm cực đại.

Lời giải: Tập xác định $D=\mathbb{R}$.
${y}’={f}'(x)=4{{x}^{3}}-4x$.
Cho ${y}’=0\Leftrightarrow x=-1\vee x=0\vee x=1.$

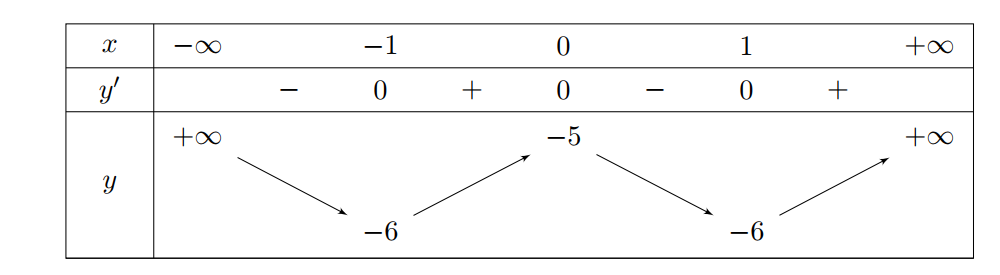
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy
(a) Đúng.
(b) Sai.
(c) Sai.
(d) Đúng.Ta có
$\begin{array}{l} f(2x)=16{{x}^{4}}-8{{x}^{2}}-5 \\ \Rightarrow {f}'(2x)=64{{x}^{3}}-16x \end{array}$
Cho ${f}'(2x)=0\Leftrightarrow x=\dfrac{-1}{2}\vee x=0\vee x=\dfrac{1}{2}$
Ta có bảng biến thiên sau:

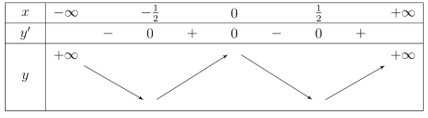
Ta thấy hàm $y=f(x)$ và $y=f(2x)$ đều đạt cực đại tại $x=0$.
(Đúng) Hàm số có 3 điểm cực trị.
(Sai) Hàm số đồng biến trên $\left( 0;+\infty \right)$.
(Sai) Điểm $M\left( 0;1 \right)$ là điểm cực tiểu của đồ thị hàm số $y=f(x)$.
(Đúng) Hàm số $y=f(x)$ và $y=f(2x)$ có cùng điểm cực đại.

Phân tích và Phương pháp giải

Dạng bài toán là nhận dạng và phân tích các tính chất của đồ thị hàm số bậc bốn trùng phương $y = ax^4 + bx^2 + c$ ($a \ne 0$). Các tính chất cần phân tích bao gồm số lượng điểm cực trị, các khoảng đồng biến/nghịch biến, tọa độ điểm cực trị và sự thay đổi cực trị khi có phép biến đổi hàm số (như $f(ax)$ hoặc $f(x)+C$). Phương pháp giải chủ yếu là sử dụng đạo hàm bậc nhất ($y’$), tìm nghiệm của $y’$, và lập bảng biến thiên để kết luận. Đối với hàm bậc bốn trùng phương, số lượng cực trị phụ thuộc vào dấu của $a$ và $b$: có 3 cực trị khi $ab < 0$, và 1 cực trị khi $ab \ge 0$. Đặc biệt, cần cẩn thận khi xác định tọa độ điểm cực trị ($x_0; f(x_0)$).

Bài toán tương tự

Tuyệt vời! Dưới đây là 5 bài toán tương tự về hàm số bậc bốn trùng phương và đồ thị hàm số, kèm đáp án chi tiết:

**1) (Tìm giá trị cực tiểu)** Cho hàm số $y={{x}^{4}}-6{{x}^{2}}+5$. Tính tổng các giá trị cực tiểu của hàm số này.
Đáp án: Tổng các giá trị cực tiểu là $-8$.
Lời giải ngắn gọn: $y’ = 4x^3 – 12x$. $y’=0 \Leftrightarrow x=0$ hoặc $x=\pm\sqrt{3}$. $f(0)=5$ (Cực đại). $f(\pm\sqrt{3}) = (\sqrt{3})^4 – 6(\sqrt{3})^2 + 5 = 9 – 18 + 5 = -4$ (Cực tiểu). Tổng các giá trị cực tiểu: $(-4) + (-4) = -8$.

**2) (Khoảng nghịch biến)** Cho hàm số $y=-2{{x}^{4}}+4{{x}^{2}}+7$. Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng $(-\infty; -1)$.
B. Hàm số đồng biến trên khoảng $(0; 1)$.
C. Hàm số nghịch biến trên khoảng $(1; +\infty)$.
D. Hàm số có 1 điểm cực đại.
Đáp án đúng: C. Hàm số nghịch biến trên khoảng $(1; +\infty)$.
Lời giải ngắn gọn: $y’ = -8x^3 + 8x = -8x(x^2 – 1)$. $y’=0 \Leftrightarrow x=0, x=\pm 1$. Hệ số $a=-2 < 0$. Hàm số có 3 cực trị. Xét dấu $y'$: $(1; +\infty) \Rightarrow x=2 \Rightarrow y'(2) = -8(2)(4-1) = -48 < 0$. Vậy hàm số nghịch biến trên $(1; +\infty)$. **3) (Điều kiện có 1 cực trị)** Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y={{x}^{4}}+2(m-1){{x}^{2}}+m$ chỉ có đúng một điểm cực trị.
A. $m < 1$.
B. $m \ge 1$.
C. $m = 1$.
D. $m \le 1$.
Đáp án đúng: B. $m \ge 1$.
Lời giải ngắn gọn: Hàm số bậc bốn trùng phương có $a=1>0$. Để hàm số chỉ có 1 cực trị thì $b$ phải không âm (tức $ab \ge 0$). Ta có $b = 2(m-1)$. Cần $2(m-1) \ge 0 \Leftrightarrow m-1 \ge 0 \Leftrightarrow m \ge 1$.

**4) (Nhận biết điểm cực trị)** Cho hàm số $y=2{{x}^{4}}-4{{x}^{2}}+3$. Khẳng định nào sau đây là sai?
A. Đồ thị hàm số có hai điểm cực tiểu là $A(-1; 1)$ và $B(1; 1)$.
B. Đồ thị hàm số đạt cực đại tại $x=0$.
C. Giá trị cực tiểu của hàm số là $-1$.
D. Hàm số đồng biến trên khoảng $(-1; 0)$.
Đáp án đúng: D. Hàm số đồng biến trên khoảng $(-1; 0)$ là SAI.
Lời giải ngắn gọn: $y’ = 8x^3 – 8x = 8x(x^2 – 1)$. $x=0, x=\pm 1$. $f(0)=3$ (Cực đại). $f(\pm 1)=2-4+3=1$ (Cực tiểu). Xét dấu $y’$: Trên $(-1; 0)$, $y’$ mang dấu âm (ví dụ $x=-0.5 \Rightarrow y’ < 0$). Vậy hàm số nghịch biến trên $(-1; 0)$. Các khẳng định A, B, C đều đúng. **5) (Hàm hợp và cực trị)** Cho hàm số $f(x) = x^4 – 8x^2$. Xét hàm số $g(x) = f(\sqrt{x})$. Tìm hoành độ các điểm cực trị của hàm số $g(x)$.
A. $x=0, x=2$.
B. $x=4$.
C. $x=0, x=4$.
D. $x=4, x=16$.
Đáp án đúng: C. $x=0, x=4$.
Lời giải ngắn gọn: $g(x) = (\sqrt{x})^4 – 8(\sqrt{x})^2 = x^2 – 8x$. (TXĐ: $x \ge 0$). $g'(x) = 2x – 8$. $g'(x)=0 \Leftrightarrow 2x – 8 = 0 \Leftrightarrow x=4$. Tuy nhiên, ta cần xét cả cực trị tại biên $x=0$. Bảng biến thiên của $g(x)$: $g(x)$ giảm từ $(0; 4)$ và tăng từ $(4; +\infty)$. Cực tiểu tại $x=4$. Cực trị tại biên $x=0$ là điểm cực đại cục bộ (giá trị lớn nhất trên lân cận $x \ge 0$). Hoành độ cực trị là $x=0$ và $x=4$.