Cho hàm số ${y=\dfrac{-x^2+x+1}{x+1}}$ có đồ thị (C).

Bài toán gốc

Cho hàm số ${y=\dfrac{-x^2+x+1}{x+1}}$ có đồ thị (C).

a) Hàm số đồng biến trên khoảng ${(-2,-1) ;(-1,0)}$.

b) Hàm số có hai điểm cực trị.

c) Đồ thị ${(C)}$ không cắt trục ${{Ox}}$.

d) Đồ thị ${(C)}$ có tiệm cận xiên đi qua điểm $A(1;2)$.

Lời giải: Ta có $y=\dfrac{-{{x}^{2}}+x+1}{x+1}=-x+2-\dfrac{1}{x+1}$
Tá có ${y^{\prime}=\dfrac{-x-2 x}{(x+1)^2}}$
${y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=-2 \end{array}\right. }$
Khi đó ta có bảng biến thiên:

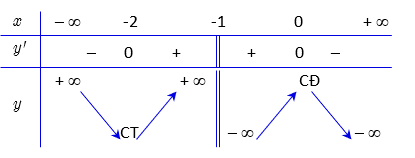
Vậy a) và b) đều đúng.
Mặt khác, ${y=0 \Leftrightarrow-x^2+x+1=0(*)}$
Vậy phương trình ${(*)}$ luôn có hai nghiệm phân biệt. Hay ${({C})}$ luôn cắt ${{Ox}}$ tại hai điểm phân biệt.
Vậy c) sai.
Tiệm cận xiên của đồ thị là $y=-x+2$
(Đúng) Hàm số đồng biến trên khoảng ${(-2,-1) ;(-1,0)}$.
(Đúng) Hàm số có hai điểm cực trị.
(Sai) Đồ thị ${(C)}$ không cắt trục ${{Ox}}$.
(Sai) Đồ thị ${(C)}$ có tiệm cận xiên đi qua điểm $A(1;2)$

Phân tích và Phương pháp giải

Dạng bài toán yêu cầu nhận dạng và phân tích các đặc điểm cơ bản của đồ thị hàm số phân thức bậc hai chia bậc nhất ($y = \frac{Ax^2+Bx+C}{Dx+E}$), bao gồm: tính đơn điệu, cực trị, tiệm cận (xiên và đứng), và giao điểm với trục tọa độ. Phương pháp giải chính là thực hiện phép chia đa thức để xác định tiệm cận xiên ($y=ax+b$) và tính đạo hàm $y’$ để tìm các điểm cực trị và xét dấu nhằm xác định khoảng đơn điệu.

Bài toán tương tự

1. Cho hàm số ${y = \frac{x^2 – 3x + 1}{x – 2}}$. Mệnh đề nào sau đây là đúng? A. Hàm số đồng biến trên khoảng $(0; 2)$. B. Hàm số đạt cực tiểu tại $x = 3$. C. Đồ thị hàm số có tiệm cận xiên là $y = x – 1$. D. Đồ thị hàm số cắt trục $Ox$ tại một điểm duy nhất. Đáp án đúng: C. Lời giải ngắn gọn: Ta có $y = x – 1 – \frac{1}{x – 2}$. Tiệm cận xiên là $y = x – 1$. Tính đạo hàm: $y’ = 1 + \frac{1}{(x-2)^2} > 0$ với mọi $x \neq 2$. Hàm số luôn đồng biến trên từng khoảng xác định và có hai nghiệm $y=0$ (hai giao điểm với Ox).
2. Cho hàm số ${y = \frac{x^2 + 4x + 3}{x + 3}}$. Khẳng định nào sau đây là sai? A. Hàm số không có cực trị. B. Đồ thị hàm số có tiệm cận đứng $x = -3$. C. Hàm số đồng biến trên các khoảng xác định. D. Đồ thị hàm số cắt trục $Oy$ tại điểm $(0; 1)$. Đáp án đúng: B. Lời giải ngắn gọn: Ta có $y = \frac{(x+1)(x+3)}{x+3}$. Với $x \neq -3$, đồ thị là đường thẳng $y = x + 1$ (bị thủng tại $x = -3$). Do đó, đồ thị không có tiệm cận đứng. Khẳng định B sai.
3. Cho hàm số ${y = \frac{2x^2 + x – 1}{x + 1}}$. Phát biểu nào sau đây là đúng? A. Hàm số có hai điểm cực trị. B. Đồ thị hàm số có tiệm cận xiên $y = 2x – 1$. C. Hàm số nghịch biến trên $(-2; -1)$. D. Đồ thị hàm số cắt trục $Ox$ tại duy nhất một điểm. Đáp án đúng: D. Lời giải ngắn gọn: Ta có $2x^2 + x – 1 = (2x – 1)(x + 1)$. Với $x \neq -1$, $y = 2x – 1$. Đây là đường thẳng bị thủng tại $x=-1$. Hàm số không có cực trị (A sai) và không có tiệm cận xiên (B sai). Hàm số đồng biến trên R trừ điểm bị thủng (C sai). Cắt Ox tại $2x – 1 = 0 \Leftrightarrow x = 1/2$. (D đúng).
4. Cho hàm số ${y = \frac{x^2 – x – 2}{x – 3}}$. Hàm số đạt cực đại, cực tiểu tại $x_1, x_2$. Giá trị của $x_1 + x_2$ bằng: A. 6. B. 8. C. 4. D. 3. Đáp án đúng: A. Lời giải ngắn gọn: Ta tính $y’ = \frac{(2x-1)(x-3) – (x^2-x-2)}{(x-3)^2} = \frac{x^2 – 6x + 5}{(x-3)^2}$. Cực trị là nghiệm của $x^2 – 6x + 5 = 0$. Theo định lý Viète, tổng hai nghiệm $x_1 + x_2 = -(-6)/1 = 6$.
5. Tìm các khoảng nghịch biến của hàm số ${y = \frac{-x^2 + 4x – 5}{x – 2}}$. A. $(1; 2)$ và $(2; 3)$. B. $(-\infty; 1)$ và $(3; +\infty)$. C. $(1; 3)$. D. $(-\infty; 2)$ và $(2; +\infty)$. Đáp án đúng: B. Lời giải ngắn gọn: Ta có $y = -x + 2 – \frac{1}{x – 2}$. Đạo hàm $y’ = -1 + \frac{1}{(x-2)^2} = \frac{-x^2 + 4x – 3}{(x-2)^2}$. $y’ = 0 \Leftrightarrow x = 1$ hoặc $x = 3$. Hàm số nghịch biến khi $y’ < 0$, tức là $-x^2 + 4x - 3 < 0$, hay $x^2 - 4x + 3 > 0$. Điều này xảy ra khi $x < 1$ hoặc $x > 3$. Khoảng nghịch biến là $(-\infty; 1)$ và $(3; +\infty)$.