Cho hàm số $f(x)=x^3-3x+1$. Các mệnh đề sau đúng hay sai?

Bài toán gốc

Cho hàm số $f(x)=x^3-3x+1$. Các mệnh đề sau đúng hay sai?

a) Đồ thị hàm số có đường tiệm cận ngang.

b) Điểm cực đại của đồ thị hàm số là $M\left( 1;-1 \right)$.

c) Hàm số đồng biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$.

d) Hàm số không có cực trị.

Lời giải: a) Tập xác định $D=\mathbb{R}$.
Ta có ${f}’\left( x \right)=3{{x}^{2}}-3$. Cho ${f}’\left( x \right)=0\Leftrightarrow 3{{x}^{2}}-3=0\Leftrightarrow \left[ \begin{array}{l} x=-1 \\ x=1 \end{array} \right.$.
Bảng biến thiên:

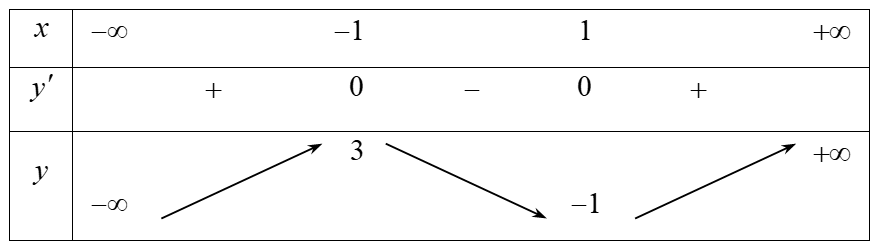
Từ bảng biến thiên suy ra đồ thị hàm số có đường tiệm cận ngang. Chọn STập xác định $D=\mathbb{R}$.
Ta có ${f}’\left( x \right)=3{{x}^{2}}-3$. Cho ${f}’\left( x \right)=0\Leftrightarrow 3{{x}^{2}}-3=0\Leftrightarrow \left[ \begin{array}{l} x=-1 \\ x=1 \end{array} \right.$.
Bảng biến thiên:

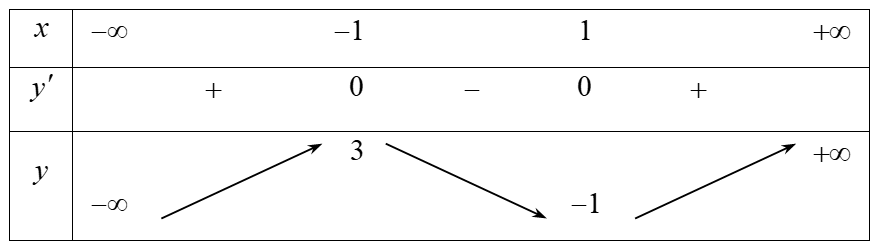
Từ bảng biến thiên suy ra điểm cực đại của đồ thị hàm số là $M\left( 1;-1 \right)$. Chọn STập xác định $D=\mathbb{R}$.
Ta có ${f}’\left( x \right)=3{{x}^{2}}-3$. Cho ${f}’\left( x \right)=0\Leftrightarrow 3{{x}^{2}}-3=0\Leftrightarrow \left[ \begin{array}{l} x=-1 \\ x=1 \end{array} \right.$.
Bảng biến thiên:

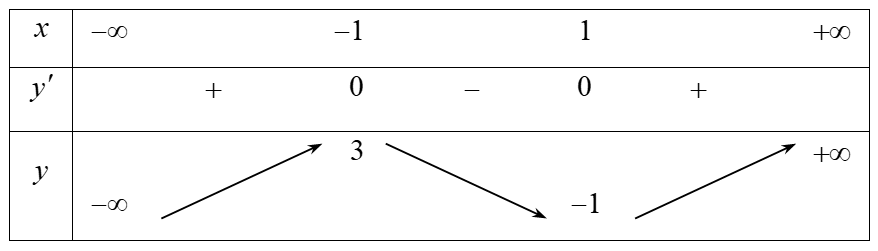
Từ bảng biến thiên suy ra hàm số đồng biến trên các khoảng $(-\infty;-1)$ và $(1;+\infty)$. Chọn ĐTập xác định $D=\mathbb{R}$.
Ta có ${f}’\left( x \right)=3{{x}^{2}}-3$. Cho ${f}’\left( x \right)=0\Leftrightarrow 3{{x}^{2}}-3=0\Leftrightarrow \left[ \begin{array}{l} x=-1 \\ x=1 \end{array} \right.$.
Bảng biến thiên:

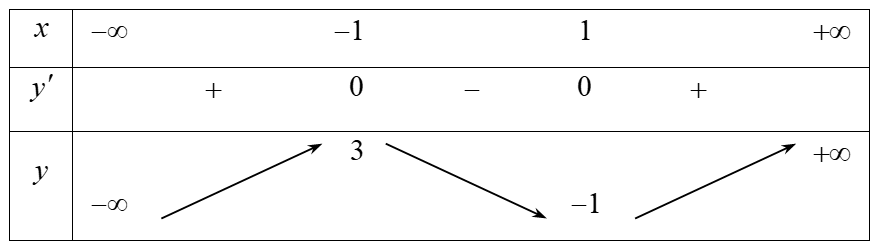
Từ bảng biến thiên suy ra hàm số không có cực trị. Chọn S
(Sai) Đồ thị hàm số có đường tiệm cận ngang.
(Sai) Điểm cực đại của đồ thị hàm số là $M\left( 1;-1 \right)$.
(Đúng) Hàm số đồng biến trên các khoảng $\left( -\infty ;-1 \right)$ và $\left( 1;+\infty \right)$.
(Sai) Hàm số không có cực trị.

Phân tích và Phương pháp giải

Đây là dạng bài tập nhận biết các tính chất cơ bản của hàm số đa thức bậc ba $y=ax^3+bx^2+cx+d$. Phương pháp giải là tính đạo hàm $f'(x)$, tìm nghiệm của $f'(x)=0$ để xác định các điểm cực trị, sau đó lập bảng biến thiên để xác định các khoảng đơn điệu. Cần lưu ý quan trọng là hàm đa thức (bậc $\ge 1$) không có bất kỳ đường tiệm cận (ngang hoặc đứng) nào.

Bài toán tương tự

Tuyệt vời! Dưới đây là 5 bài toán tương tự:

**Câu 1:** Cho hàm số $f(x)=x^3-6x^2+9x+1$. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng $(1; 3)$.
B. Hàm số đạt cực tiểu tại $x=1$.
C. Đồ thị hàm số có đường tiệm cận ngang.
D. Hàm số đồng biến trên khoảng $(1; 3)$.

**Đáp án đúng: A.**
Lời giải ngắn gọn: Ta có $f'(x) = 3x^2 – 12x + 9$. Cho $f'(x)=0 \Leftrightarrow x=1$ hoặc $x=3$. Vì hệ số $a=1>0$, hàm số nghịch biến (giảm) trên khoảng giữa hai nghiệm, tức là $(1; 3)$.

**Câu 2:** Cho hàm số $y=-x^3+3x^2+4$. Khẳng định nào sau đây là sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số đồng biến trên khoảng $(0; 2)$.
C. Điểm cực tiểu của đồ thị hàm số là $(0; 4)$.
D. Đồ thị hàm số có đường tiệm cận đứng.

**Đáp án đúng: D.**
Lời giải ngắn gọn: Ta có $y’ = -3x^2 + 6x$. Hàm số có hai cực trị tại $x=0$ và $x=2$. Tuy nhiên, vì đây là hàm đa thức, đồ thị của nó không có tiệm cận đứng hay tiệm cận ngang. Mệnh đề D sai.

**Câu 3:** Cho hàm số $y = \frac{1}{3}x^3 – x^2 – 3x + 5$. Tổng hoành độ các điểm cực trị của hàm số là:
A. 2.
B. 3.
C. -2.
D. 1.

**Đáp án đúng: A.**
Lời giải ngắn gọn: Hoành độ các điểm cực trị là nghiệm của phương trình $y’ = x^2 – 2x – 3 = 0$. Áp dụng định lý Vi-ét, tổng các nghiệm (hoành độ cực trị) là $x_1 + x_2 = -(-2)/1 = 2$.

**Câu 4:** Xét hàm số $y = -x^3 + 9x^2 – 15x + 3$. Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng $(1; 5)$.
B. Hàm số nghịch biến trên khoảng $(-\infty; 1)$.
C. Hàm số đạt cực đại tại $x=1$.
D. Hàm số đạt cực tiểu tại $x=5$.

**Đáp án đúng: A.**
Lời giải ngắn gọn: Ta có $y’ = -3x^2 + 18x – 15 = -3(x^2 – 6x + 5)$. Nghiệm của $y’=0$ là $x=1$ và $x=5$. Vì hệ số của $x^3$ là $a=-1 < 0$, hàm số đồng biến (tăng) trên khoảng giữa hai nghiệm, tức là $(1; 5)$. **Câu 5:** Cho hàm số $y = x^3 + 3x^2 – 4$. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
(I) Hàm số có giá trị cực đại là $0$.
(II) Đồ thị hàm số có một đường tiệm cận ngang.
(III) Hàm số nghịch biến trên khoảng $(-2; 0)$.
(IV) Hàm số không có cực trị.
A. 1.
B. 2.
C. 3.
D. 4.

**Đáp án đúng: B.**
Lời giải ngắn gọn: Ta có $y’ = 3x^2 + 6x = 3x(x+2)$. Cực trị tại $x=-2$ và $x=0$. $y(-2)=0$ (cực đại), $y(0)=-4$ (cực tiểu).
(I) $y_{CD}=0$. Đúng.
(II) Hàm đa thức, không có TCN. Sai.
(III) $y'<0$ trên $(-2; 0)$. Hàm nghịch biến. Đúng.
(IV) Hàm có 2 cực trị. Sai.
Vậy có 2 mệnh đề đúng: (I) và (III).