Cho hàm số $y=f(x)=ax^3+bx^2+cx+d,a\neq 0$ có đồ thị như hình dưới đây:

Chọn phát biểu đúng?

Bài toán gốc

Cho hàm số $y=f(x)=ax^3+bx^2+cx+d,a\neq 0$ có đồ thị như hình dưới đây:

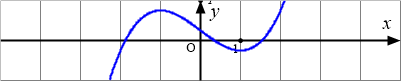
Chọn phát biểu đúng?

A. $a{>}0,d{>}0$.B. $a{<}0,d{<}0$.C. $a{<}0,d{>}0$.D. $a{>}0,d{<}0$.

Phân tích và Phương pháp giải

Dạng toán nhận biết dấu các hệ số $a, b, c, d$ của hàm đa thức bậc ba $y=ax^3+bx^2+cx+d$ dựa vào đồ thị hàm số.
1. Dấu của $a$: Xác định dựa vào chiều biến thiên khi $x \to \pm\infty$. Đồ thị ban đầu có nhánh ngoài cùng bên phải đi xuống, suy ra $a<0$.
2. Dấu của $d$: Xác định dựa vào giao điểm của đồ thị với trục tung ($y$-intercept), vì $f(0)=d$. Đồ thị cắt trục tung tại điểm có tung độ dương, suy ra $d>0$.
3. Kết luận: $a<0$ và $d>0$. (Đáp án C).

Bài toán tương tự

Câu 1: Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị như sau: Đồ thị đi lên từ trái sang phải ở nhánh ngoài cùng bên phải, và cắt trục tung tại điểm có tung độ âm. Chọn phát biểu đúng về dấu của $a$ và $d$.

A. $a<0, d<0$. B. $a>0, d>0$. C. $a<0, d>0$. D. $a>0, d<0$.

Đáp án đúng: D. Giải thích: Nhánh phải đi lên $\implies a>0$. Cắt trục tung tại điểm âm $\implies d=f(0)<0$.

---

Câu 2: Đồ thị của hàm số bậc ba $y=ax^3+bx^2+cx+d$ có dạng: nhánh ngoài cùng bên phải đi xuống, và giao điểm với trục tung nằm dưới gốc tọa độ. Mệnh đề nào sau đây là đúng?

A. $a>0, d<0$. B. $a<0, d>0$. C. $a<0, d<0$. D. $a>0, d>0$.

Đáp án đúng: C. Giải thích: Nhánh phải đi xuống $\implies a<0$. Giao điểm y dưới gốc tọa độ $\implies d=f(0)<0$.

---

Câu 3: Cho hàm số $y=ax^3+bx^2+cx+d$. Đồ thị hàm số có nhánh ngoài cùng bên phải đi xuống, và tiếp tuyến tại giao điểm với trục tung có hệ số góc dương (tức là đồ thị đồng biến tại $x=0$). Chọn phát biểu đúng về dấu của $a$ và $c$.

A. $a<0, c>0$. B. $a>0, c>0$. C. $a<0, c<0$. D. $a>0, c<0$.

Đáp án đúng: A. Giải thích: Nhánh phải đi xuống $\implies a<0$. Tiếp tuyến tại $x=0$ dốc lên (hàm đồng biến) $\implies c=f'(0)>0$.

---

Câu 4: Cho hàm số $y=ax^3+bx^2+cx+d$. Đồ thị có nhánh ngoài cùng bên phải đi lên. Hai điểm cực trị $x_1, x_2$ thỏa mãn $x_1+x_2 < 0$ (hay điểm uốn $x_u < 0$). Phát biểu nào sau đây đúng?

A. $a>0, b<0$. B. $a<0, b>0$. C. $a>0, b>0$. D. $a<0, b<0$.

Đáp án đúng: C. Giải thích: Nhánh phải đi lên $\implies a>0$. Hoành độ điểm uốn $x_u = -b/(3a)$. Vì $x_1+x_2<0$ nên $x_u<0$. Ta có $a>0$ và $x_u = -b/(3a) < 0$. Suy ra $-b < 0 \implies b > 0$.

---

Câu 5: Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị như sau: Nhánh ngoài cùng bên phải đi lên. Đồ thị cắt trục tung tại điểm dương. Điểm cực đại và cực tiểu đều nằm bên trái trục tung (tức là $x_1<0, x_2<0$). Tại giao điểm với trục tung, đồ thị đang nghịch biến. Phát biểu nào sau đây là đúng?

A. $a>0, b>0, c<0, d>0$. B. $a>0, b<0, c>0, d>0$. C. $a<0, b<0, c<0, d<0$. D. $a>0, b>0, c>0, d<0$.

Đáp án đúng: A. Giải thích: 1. $a$: Nhánh phải đi lên $\implies a>0$. 2. $d$: Cắt trục tung tại điểm dương $\implies d>0$. 3. $c$: Tại $x=0$, đồ thị nghịch biến $\implies c=f'(0)<0$. 4. $b$: Hai cực trị $x_1, x_2$ đều âm. $x_1+x_2 = -2b/(3a)$. Vì $x_1+x_2<0$ và $a>0$, suy ra $-2b<0 \implies b>0$. Kết luận: $a>0, b>0, c<0, d>0$.