Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, tam giác \(SAD\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy \(ABCD\). Biết \(SD = a\), gọi \(K\) là trung điểm của \(AB\), góc giữa đường thẳng \(SK\) với mặt phẳng đáy bằng \(60^\circ \). Tính thể tích V của khối chóp \(S.ABCD\). A. \(V = \frac{{4{a^3}\sqrt {42} }}{{49}}\) B. \(V = \frac{{2{a^3}\sqrt … [Đọc thêm...] vềCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, tam giác \(SAD\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy \(ABCD\). Biết \(SD = a\), gọi \(K\) là trung điểm của \(AB\), góc giữa đường thẳng \(SK\) với mặt phẳng đáy bằng \(60^\circ \). Tính thể tích V của khối chóp \(S.ABCD\).
Trắc nghiệm Thể tích đa diện
nbsp; Trong không gian cho tam giác đều \(SAB\) và hình chữ nhật \(ABCD\) với\(AD = 2a\) nằm trên hai mặt phẳng vuông góc. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Biết \(\tan \varphi = \frac{{2\sqrt 2 }}{3}\). Thể tích của khối chóp \(S.ABC\) là
nbsp; Trong không gian cho tam giác đều \(SAB\) và hình chữ nhật \(ABCD\) với\(AD = 2a\) nằm trên hai mặt phẳng vuông góc. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Biết \(\tan \varphi = \frac{{2\sqrt 2 }}{3}\). Thể tích của khối chóp \(S.ABC\) là A. \(V = {a^3}\sqrt 3 \) B. \(V = \frac{{{a^3}\sqrt 3 }}{2}\) C. … [Đọc thêm...] vềnbsp; Trong không gian cho tam giác đều \(SAB\) và hình chữ nhật \(ABCD\) với\(AD = 2a\) nằm trên hai mặt phẳng vuông góc. Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\). Biết \(\tan \varphi = \frac{{2\sqrt 2 }}{3}\). Thể tích của khối chóp \(S.ABC\) là
Cho khối lăng trụ \(ABC.{A’}{B’}{C’}\) có đáy là tam giác vuông cân tại \(A,{A’}A = {A’}B = {A’}C = a\). Biết diện tích \(\Delta {A’}BC = \frac{{\sqrt 3 {a^2}}}{4}\), thể tích khối lăng trụ đã cho bằng
Cho khối lăng trụ \(ABC.{A'}{B'}{C'}\) có đáy là tam giác vuông cân tại A, \({A'}A = {A'}B = {A'}C = a\). Biết diện tích \(\Delta {A'}BC = \frac{{\sqrt 3 {a^2}}}{4}\), thể tích khối lăng trụ đã cho bằng A.\(\frac{{\sqrt 3 {a^2}}}{{24}}\) B. \(\frac{{\sqrt 3 {a^3}}}{8}\) C.\(\frac{{3{a^3}}}{8}\) D.\(\frac{{{a^3}}}{8}\). Lời giải: Gọi \(H\) là trung điểm của … [Đọc thêm...] vềCho khối lăng trụ \(ABC.{A’}{B’}{C’}\) có đáy là tam giác vuông cân tại \(A,{A’}A = {A’}B = {A’}C = a\). Biết diện tích \(\Delta {A’}BC = \frac{{\sqrt 3 {a^2}}}{4}\), thể tích khối lăng trụ đã cho bằng
Cho lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều cạnh \(a\), hình chiếu vuông góc của điểm \(A’\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA’\) và \(BC\) bằng \(\frac{{a\sqrt 3 }}{4}\). Tính theo \(a\) thể tích khối lăng trụ đó.
Cho lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\), hình chiếu vuông góc của điểm \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA'\) và \(BC\) bằng \(\frac{{a\sqrt 3 }}{4}\). Tính theo \(a\) thể tích khối lăng trụ đó. A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\). B. \(\frac{{{a^3}\sqrt 3 … [Đọc thêm...] vềCho lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều cạnh \(a\), hình chiếu vuông góc của điểm \(A’\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA’\) và \(BC\) bằng \(\frac{{a\sqrt 3 }}{4}\). Tính theo \(a\) thể tích khối lăng trụ đó.
Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Gọi \(E\) là một điểm thuộc cạnh \(DD’\) sao cho \(\tan \left( {BE;\left( {CDD’} \right)} \right) = \frac{3}{{\sqrt {13} }}\). Thể tích của khối tứ diện \(EB’AC\) bằng
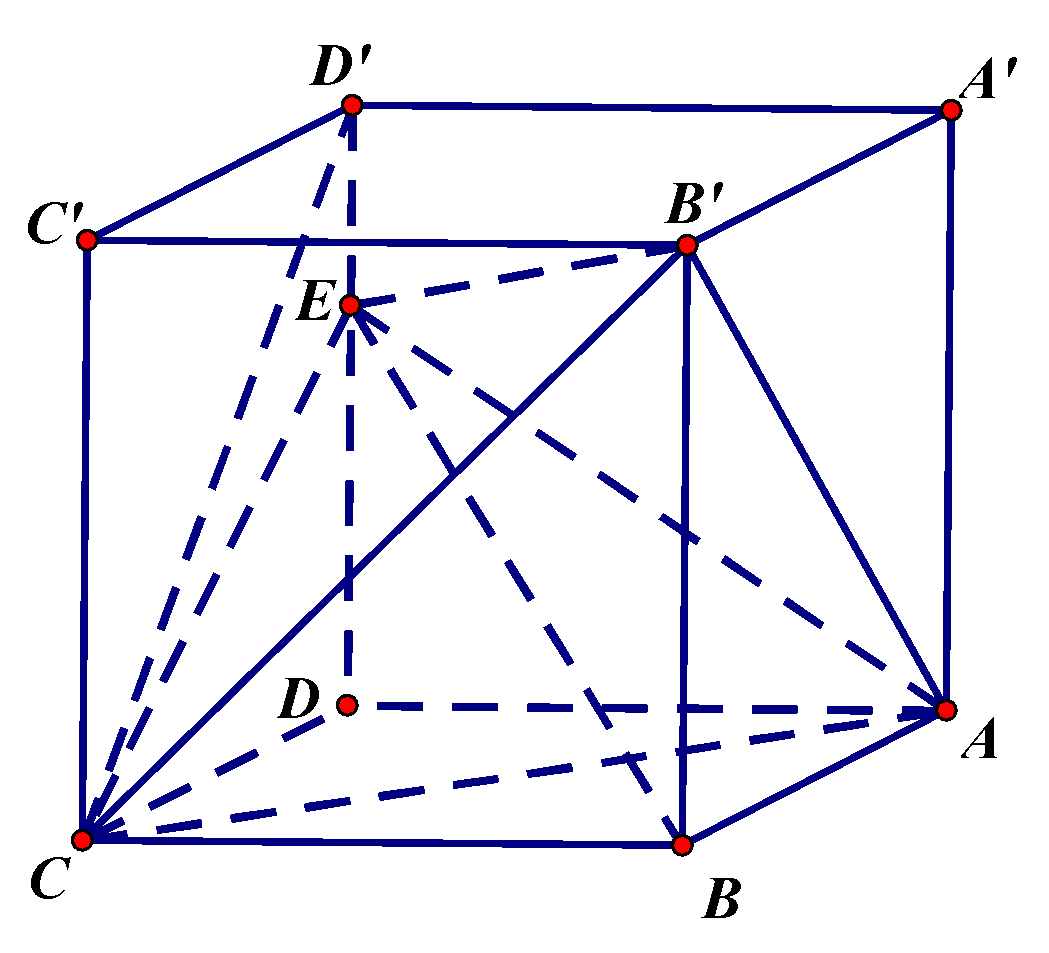
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(E\) là một điểm thuộc cạnh \(DD'\) sao cho \(\tan \left( {BE;\left( {CDD'} \right)} \right) = \frac{3}{{\sqrt {13} }}\). Thể tích của khối tứ diện \(EB'AC\) bằng
A. \(\frac{{5{a^3}}}{{18}}\)
B. \(\frac{{2{a^3}}}{3}\)
C. \(\frac{{6{a^3}}}{{\sqrt {38} }}\)
D. \(\frac{{\sqrt {19} {a^3}}}{3}\)
Lời … [Đọc thêm...] về Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Gọi \(E\) là một điểm thuộc cạnh \(DD’\) sao cho \(\tan \left( {BE;\left( {CDD’} \right)} \right) = \frac{3}{{\sqrt {13} }}\). Thể tích của khối tứ diện \(EB’AC\) bằng