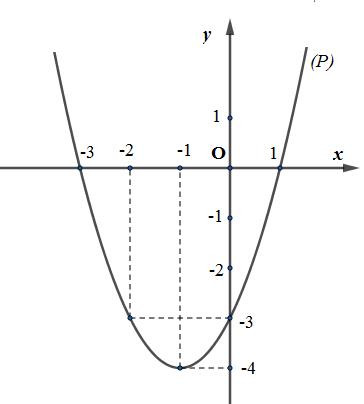
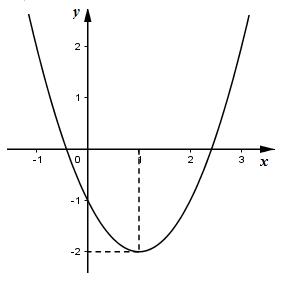
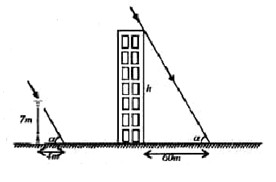
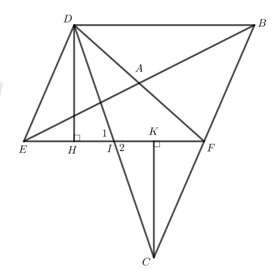
Đề thi mẫu HK1 Toán lớp 10 – số 3 --- 12 --- Đề bài PHẦN 1. TRẮC NGHIỆM (3 điểm) Câu 1 : Cho hai tập hợp \(\left( {1;3} \right)\) và \(\left[ {2;4} \right]\). Giao của hai tập hợp đã cho là: A. \(\left( {2;3} \right]\). B. \(\left( {2;3} \right)\). C. \(\left[ {2;3} \right)\). D. \(\left[ {2;3} \right]\). … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 10 – số 3
Kết quả tìm kiếm cho: ty so
Đề thi mẫu HK1 Toán lớp 10 – số 2
Đề thi mẫu HK1 Toán lớp 10 – số 2 --- 13 --- Đề bài A. PHẦN TRẮC NGHIỆM (8 điểm) Câu 1 : Trong mặt phẳng tọa độ Oxy, cho các vectơ \(\overrightarrow u = \left( {2; - 4} \right);\,\,\overrightarrow a = \left( { - 1; - 2} \right);\)\(\,\,\overrightarrow b = \left( {1; - 3} \right)\). Biết \(\overrightarrow u = m\overrightarrow a + n\overrightarrow b \), tính … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 10 – số 2
Đề thi mẫu HK1 Toán lớp 10 – số 1
Đề thi mẫu HK1 Toán lớp 10 – số 1 --- 14--- Đề bài I.PHẦN CÂU HỎI TRẮC NGHIỆM (5 ĐIỂM) Câu 1 . Tập nghiệm của phương trình \(\sqrt { - {x^2} + 4x} + 2 = 2x\) là A. \(S = \mathbb{R}\) B. \(S = \emptyset \) C. \(S = \left\{ {\dfrac{2}{5};2} \right\}\) D. \(S = \left\{ 2 \right\}\) Câu 2 . Cho\(A = \left\{ {1,2,3,4,5,6} \right\},B = … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 10 – số 1
Đề thi mẫu HK1 Toán lớp 9 – số 5
Đề thi mẫu HK1 Toán lớp 9 – số 5 ---16-- Đề bài Câu 1 (1,5 điểm): Thực hiện phép tính a) \(2\sqrt {50} - 3\sqrt {32} - \sqrt {162} + 5\sqrt {98} \) b) \(\sqrt {8 + 2\sqrt 7 } + \sqrt {11 - 4\sqrt 7 } \) c) \(\dfrac{{10}}{{\sqrt 5 }} + \dfrac{8}{{3 + \sqrt 5 }} - \dfrac{{\sqrt {18} - 3\sqrt 5 }}{{\sqrt 2 - \sqrt 5 }}\) Câu 2 (2,0 điểm): … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 9 – số 5
Đề thi mẫu HK1 Toán lớp 7 – số 5
Đề thi mẫu HK1 Toán lớp 7 – số 4 --- 12--- Đề bài Câu 1 (1 điểm): a) Cho y tỉ lệ thuận với x, biết \(x = - 8\)thì \(y = \dfrac{2}{3}\). Tính hệ số tỉ lệ k. b) Cho y tỉ lệ nghịch với x, biết \(x = \dfrac{{ - 4}}{3}\)thì \(y = - 12\). Tính hệ số tỉ lệ a. Câu 2 (1,5điểm): Tính hợp lý (nếu có thể) a) \(\dfrac{{ - 2}}{3} + 75\% - 5\dfrac{1}{4} + {\left( … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 7 – số 5
Đề thi mẫu HK1 Toán lớp 3 – số 1
Ma trận Đề thi học kì 1 lớp 3 môn Toán năm 2019 - 2020 theo Thông tư 22 Mạch kiến thức, kĩ năng Số câu và số điểm Mức 1 Mức 2 Mức 3 Mức 4 Tổng T N KQ T L TN KQ T L TN KQ T L TN KQ T L TN KQ T L Số học Số câu 1 2 1 1 3 2 Số điểm … [Đọc thêm...] vềĐề thi mẫu HK1 Toán lớp 3 – số 1
Ôn tập cuối năm – Đại số – Giải tích 11
1. Phần đại số a) Hàm số lượng giác Hàm số lượng giác: Hàm số sin, hàm số cos, hàm số tang, hàm số cotang. Phương trình lượng giác: Phương trình lượng giác cơ bản theo sin, cos, tan, cot. Các dạng phương trình lượng giác thường gặp: Phương trình lượng giác đưa về dạng đại số. Phương trình bậc nhất đối với sin và cos. Phương trình chứa tổng (hay hiêu) … [Đọc thêm...] vềÔn tập cuối năm – Đại số – Giải tích 11
Bài 1: Định nghĩa và ý nghĩa của đạo hàm – Chương 5 – Đại số 11
1. Định nghĩa đạo hàm tại một điểm a) Định nghĩa Cho hàm số \(y=f(x)\) xác định trên khoảng \((a;b)\)và \(x_0 \in (a;b)\), đạo hàm của hàm số tại điểm \(x_0\) là: \(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) – f({x_0})}}{{x – {x_0}}}.\) b) Chú ý Nếu kí hiệu \(\Delta x = x – {x_0};\,\,\Delta y = f({x_0} + \Delta x) – f({x_0})\) thì: \(f'({x_0}) = \mathop … [Đọc thêm...] vềBài 1: Định nghĩa và ý nghĩa của đạo hàm – Chương 5 – Đại số 11
Ôn tập Chương 4 – Đại số 11
GIỚI HẠN CỦA DÃY SỐ I. KIẾN THỨC CƠ BẢN 1. Định nghĩa Định nghĩa 1: Ta nói rằng dãy số (un) có giới hạn là 0 khi n dần tới vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ số hạng nào đó trở đi. Kí hiệu:\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}} \right) = 0{\rm{ \, hay \, }}{{\rm{u}}_{\rm{n}}} \to 0{\rm{ \, khi\, n}} … [Đọc thêm...] vềÔn tập Chương 4 – Đại số 11
Bài 3. Hàm số liên tục – Chương 4 – Đại số 11
1. Định nghĩa \( \bullet \) Cho hàm số \(y = f(x)\) xác định trên khoảng K và \({x_0} \in K\) 1) Hàm số \(y = f(x)\) liên tục tại \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\) 2) Hàm số \(y = f(x)\) không liên tục tại \({x_0}\) ta nói hàm số gián đoạn tại \({x_0}\) \( \bullet \) \(y = f(x)\) liên tục trên một khoảng nếu nó kiên tục tại … [Đọc thêm...] vềBài 3. Hàm số liên tục – Chương 4 – Đại số 11