Sách giáo khoa NXB Giáo dục/File nén 1-12 - Sách Giáo Khoa lớp 12 ================ Sách Giáo Khoa lớp 12 NXB Giáo dục trong có SGK lớp 1,2,6 theo chương trình mới GDPT 2018 ĐÂY LÀ FILE NÉN RAR CÁC BẠN TẢI VỀ XẢ NÉN RA SỬ DỤNG CHO MÙA COVID-2021 ============= Sách giáo khoa Giải tích 12 cơ bản Sách giáo khoa Hình học 12 cơ bản Sách Bài tập giải tích 12 … [Đọc thêm...] vềSách Giáo Khoa lớp 12
Blog
Sách Giáo Khoa lớp 9
Sách giáo khoa NXB Giáo dục/File nén 9 - Sách Giáo Khoa lớp 9 ================ Sách Giáo Khoa lớp 9 NXB Giáo dục trong có SGK lớp 1,2,6 theo chương trình mới GDPT 2018 ĐÂY LÀ FILE NÉN RAR CÁC BẠN TẢI VỀ XẢ NÉN RA SỬ DỤNG CHO MÙA COVID-2021 Sách giáo khoa toán 9 tập 1 Sách bài tập toán 9 tập 2 Sách bài tập toán 9 tập 1 Sách giáo khoa toán 9 tập … [Đọc thêm...] vềSách Giáo Khoa lớp 9
Sách Giáo Khoa lớp 5
Sách giáo khoa NXB Giáo dục/File nén 5 - Sách Giáo Khoa lớp 5 ================ Sách Giáo Khoa lớp 5 NXB Giáo dục trong có SGK lớp 1,2,6 theo chương trình mới GDPT 2018 ĐÂY LÀ FILE NÉN RAR CÁC BẠN TẢI VỀ XẢ NÉN RA SỬ DỤNG CHO MÙA COVID-2021 Sách giáo khoa toán lớp 5 Vở bài tập Toán lớp 5 – Tập 2 Vở bài tập Toán lớp 5 – Tập 1 ============= thu … [Đọc thêm...] vềSách Giáo Khoa lớp 5
Cho khối lăng trụ tam giác đều \(ABC.A’B’C’\) có cạnh bên bằng \(2a\) , góc giữa hai mặt phẳng \(\left( {A’BC} \right)\) và \(\left( {ABC} \right)\) bằng
Câu hỏi: Cho khối lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh bên bằng \(2a\) , góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \) . Thể tích của khối lăng trụ đã cho bằng A. \(\frac{{8\sqrt 3 }}{{27}}{a^3}\) . B. \(8\sqrt 3 {a^3}\) . C. \(\frac{{8\sqrt 3 }}{3}{a^3}\) . D. \(\frac{{8\sqrt 3 }}{9}{a^3}\) . LỜI … [Đọc thêm...] vềCho khối lăng trụ tam giác đều \(ABC.A’B’C’\) có cạnh bên bằng \(2a\) , góc giữa hai mặt phẳng \(\left( {A’BC} \right)\) và \(\left( {ABC} \right)\) bằng
Trong không gian \(Oxyz\) cho điểm \(A\left( {1;1;1} \right)\) và đường thẳng \(d:\frac{{x – 1}}{1} = \frac{y}{2} = \frac{{z + 1}}{1}\) . Đường thẳng đi qua \(A\) , cắt trục \(Oy\) và vuông góc với \(d\) có phương trình là
Câu hỏi: Trong không gian \(Oxyz\) cho điểm \(A\left( {1;1;1} \right)\) và đường thẳng \(d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z + 1}}{1}\) . Đường thẳng đi qua \(A\) , cắt trục \(Oy\) và vuông góc với \(d\) có phương trình là A. \(\left\{ \begin{array}{l}x = - 1 + t\\y = 3 - t\\z = - 1 + t\end{array} \right.\) . B. \(\left\{ \begin{array}{l}x = 1 - … [Đọc thêm...] vềTrong không gian \(Oxyz\) cho điểm \(A\left( {1;1;1} \right)\) và đường thẳng \(d:\frac{{x – 1}}{1} = \frac{y}{2} = \frac{{z + 1}}{1}\) . Đường thẳng đi qua \(A\) , cắt trục \(Oy\) và vuông góc với \(d\) có phương trình là
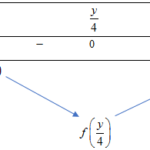
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2}\left( {a,b,c \in \mathbb{R}} \right).\) Hàm số \(y = f’\left( x \right)\) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình \(2f\left( x \right) + 3 = 0\)
Câu hỏi: Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2}\left( {a,b,c \in \mathbb{R}} \right).\) Hàm số \(y = f'\left( x \right)\) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình \(2f\left( x \right) + 3 = 0\) A. \(4\) . B. \(1\) . C. \(2\) . D. \(3\) . LỜI GIẢI CHI TIẾT Giả sử đồ thị hàm số \(y = f'\left( … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2}\left( {a,b,c \in \mathbb{R}} \right).\) Hàm số \(y = f’\left( x \right)\) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình \(2f\left( x \right) + 3 = 0\)
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) – {{\log }_2}\left( {x + 21} \right)} \right]\left( {16 – {2^{x – 1}}} \right) \ge 0\) ?
Câu hỏi: Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) - {{\log }_2}\left( {x + 21} \right)} \right]\left( {16 - {2^{x - 1}}} \right) \ge 0\) ? A. Vô số. B. \[17\] . C. \[16\] . D. \[18\] . LỜI GIẢI CHI TIẾT Điều kiện: \(x > - 21\) Có \[\left[ {{{\log }_2}\left( {{x^2} + 1} \right) - {{\log }_2}\left( … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) – {{\log }_2}\left( {x + 21} \right)} \right]\left( {16 – {2^{x – 1}}} \right) \ge 0\) ?
Cho hàm số \(f\left( x \right) = {x^4} – 10{x^3} + 24{x^2} + \left( {4 – m} \right)x\) , với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng \(7\) điểm cực trị.
Câu hỏi: Cho hàm số \(f\left( x \right) = {x^4} - 10{x^3} + 24{x^2} + \left( {4 - m} \right)x\) , với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng \(7\) điểm cực trị. A. \(26\) . B. \(25\) . C. \(22\) . D. \(21\) . LỜI GIẢI CHI TIẾT Có \(f'\left( … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^4} – 10{x^3} + 24{x^2} + \left( {4 – m} \right)x\) , với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng \(7\) điểm cực trị.
Cho hai hàm số \(f(x) = a{x^4} + b{x^3} + c{x^2} + x\) và \(g(x) = m{x^3} + n{x^2} – 2x\) ; với \(a,b,c,m,n \in \mathbb{R}\) . Biết hàm số \(y = f(x) – g(x)\) có ba điểm cực trị là \( – 1,2\) và 3. Diện tích hình phẳng giới hạn bởi hai đương \(y = f'(x)\) và \(y = g'(x)\) bằng
Câu hỏi: Cho hai hàm số \(f(x) = a{x^4} + b{x^3} + c{x^2} + x\) và \(g(x) = m{x^3} + n{x^2} - 2x\) ; với \(a,b,c,m,n \in \mathbb{R}\) . Biết hàm số \(y = f(x) - g(x)\) có ba điểm cực trị là \( - 1,2\) và 3. Diện tích hình phẳng giới hạn bởi hai đương \(y = f'(x)\) và \(y = g'(x)\) bằng A. \(\frac{{16}}{3}\) . B. \(\frac{{71}}{6}\) . C. … [Đọc thêm...] vềCho hai hàm số \(f(x) = a{x^4} + b{x^3} + c{x^2} + x\) và \(g(x) = m{x^3} + n{x^2} – 2x\) ; với \(a,b,c,m,n \in \mathbb{R}\) . Biết hàm số \(y = f(x) – g(x)\) có ba điểm cực trị là \( – 1,2\) và 3. Diện tích hình phẳng giới hạn bởi hai đương \(y = f'(x)\) và \(y = g'(x)\) bằng
Có bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right)\) ?
Câu hỏi: Có bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x - 1} \right){e^x} = y\left( {{e^x} + xy - 2{x^2} - 3} \right)\) ? A. 17 . B. 18 . C. 16 . D. 15 . LỜI GIẢI CHI TIẾT Ta có \(4\left( {x - 1} \right){e^x} = y\left( {{e^x} + xy - 2{x^2} - 3} \right) \Leftrightarrow 4\left( {x - 1} \right){e^x} - … [Đọc thêm...] vềCó bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right)\) ?