Có bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right)\) ?

Câu hỏi:
Có bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right)\) ?

A. 17 .

B. 18 .

C. 16 .

D. 15 .

LỜI GIẢI CHI TIẾT

Ta có \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right) \Leftrightarrow 4\left( {x – 1} \right){e^x} – y\left( {{e^x} + xy – 2{x^2} – 3} \right) = 0\) .

Xét hàm số \(f\left( x \right) = 4\left( {x – 1} \right){e^x} – y\left( {{e^x} + xy – 2{x^2} – 3} \right)\)  với biến số \(x \in \left( {1;\,6} \right)\)  và tham số \(y \in {\mathbb{N}^ * }\) .

\(f’\left( x \right) = \left( {4x – y} \right)\left( {{e^x} + y} \right)\) . \(f’\left( x \right) = 0 \Leftrightarrow x = \frac{y}{4}\) .

\(f\left( 1 \right) = y\left( {5 – e – y} \right)\) , \(f\left( 6 \right) = – 6{y^2} + \left( {75 – {e^6}} \right)y + 20{e^6}\) , \(f\left( {\frac{y}{4}} \right) = – 4{e^{\frac{y}{4}}} – \frac{{{y^3}}}{8} + 3y\) .

∙) Trường hợp 1: \(\frac{y}{4} \notin \left( {1;\,6} \right) \Leftrightarrow \left[ \begin{array}{l}y \le 4\\y \ge 24\end{array} \right.\)

+) Với \(y \le 4\) ta có \(f’\left( x \right) > 0\,\forall \,x \in \left( {1;\,6} \right) \Rightarrow f\left( x \right) \in \left( {f\left( 1 \right);\,f\left( 6 \right)} \right)\) . Khi đó phương trình \(f\left( x \right) = 0\) có nghiệm khi và chỉ khi \(\left\{ \begin{array}{l}f\left( 1 \right) < 0\\f\left( 6 \right) > 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}y = 3\\y = 4\end{array} \right.\) .

+) Với \(y \ge 24\) ta có \(f’\left( x \right) < 0\,\forall \,x \in \left( {1;\,6} \right) \Rightarrow f\left( x \right) \in \left( {f\left( 6 \right);\,f\left( 1 \right)} \right)\) .

Do \(f\left( 1 \right) < 0\) nên phương trình vô nghiệm khi \(y \ge 24\) .

∙) Trường hợp 2: \(\frac{y}{4} \in \left( {1;\,6} \right) \Leftrightarrow y \in \left( {4;\,24} \right)\) .

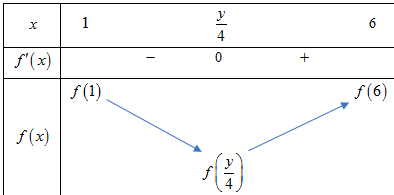
Ta có bảng biến thiên:

Vì \(f\left( 1 \right) < 0\) nên phương trình có nghiệm khi \(f\left( 6 \right) > 0 \Leftrightarrow 6{y^2} – \left( {75 – e} \right)y – 20{e^6} < 0\) \( \Leftrightarrow y \in \left( {{y_1};\,{y_2}} \right)\), với \({y_1} = \frac{{75 – {e^6} – \sqrt {{e^{12}} + 330{e^6} + 5625} }}{{12}},{y_2} = \frac{{75 – {e^6} + \sqrt {{e^{12}} + 330{e^6} + 5625} }}{{12}}\) Suy ra \(y \in \left\{ {5;\,6;\,…;\,17,18} \right\}\). Kết hợp 2 trường hợp ta được \(y \in \left\{ {3;\,4;5;\,…;\,17,18} \right\}\). Chọn đáp án C.