Cho các số thực \(x,y,a,b\) thỏa mãn điều kiện \(x > 1,y > 1,a > 0,b > 0\), \(x + y = xy\). Biết rằng biểu thức \(P = \frac{{y{a^x} + x{b^y}}}{{abxy}}\) đạt giá trị nhỏ nhất \(m\) khi \(a = {b^q}\). Khẳng định nào sau đây đúng ?

Cho các số thực \(x,y,a,b\) thỏa mãn điều kiện \(x > 1,y > 1,a > 0,b > 0\), \(x + y = xy\). Biết rằng biểu thức \(P = \frac{{y{a^x} + x{b^y}}}{{abxy}}\) đạt giá trị nhỏ nhất \(m\) khi \(a = {b^q}\). Khẳng định nào sau đây đúng ?

A. \(m + \frac{1}{q} = \frac{y}{{y – 1}}\).         B. \(m + \frac{1}{q} = \frac{x}{{x – 1}}\).    C. \(m + \frac{1}{q} = \frac{{y – 1}}{y}\).             D. \(m + \frac{1}{q} = y\) .

BÀI GIẢI

Ta có \(P = \frac{{{a^{x – 1}}}}{{bx}} + \frac{{{b^{y – 1}}}}{{ay}} = f\left( a \right)\), suy ra \(f’\left( a \right) = \frac{{x – 1}}{{bx}}{a^{x – 2}} – \frac{{{b^{y – 1}}}}{{y{a^2}}} = 0 \Leftrightarrow {a^x} = {b^y} \Leftrightarrow x.\ln a = y.\ln b\) \( \Leftrightarrow \ln a = \frac{y}{x}\ln b \Leftrightarrow a = {b^{\frac{y}{x}}} \Leftrightarrow a = {b^{y – 1}}\)

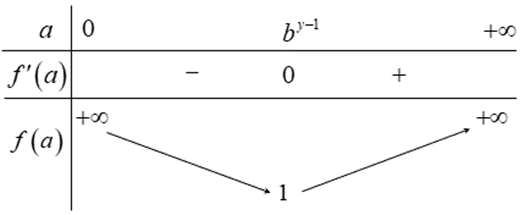
\(f\left( {{b^{y – 1}}} \right) = 1\), \(\mathop {\lim }\limits_{a \to {0^ + }} f\left( a \right) =  + \infty ,\mathop {\lim }\limits_{a \to  + \infty } f\left( a \right) =  + \infty \)

Ta có BBT

Từ BBT\( \Rightarrow \min P = 1\), đạt được khi \(a = {b^{y – 1}}\).

Do đó \(m = 1,q = y – 1 \Rightarrow m + \frac{1}{q} = \frac{y}{{y – 1}}\).