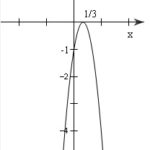
Đề bài: Vẽ đồ thị hàm số $y = - 9x^2 + 6x - 1$ Lời giải Hướng dẫn:Trục đối xứng $x= - \frac{b}{2a} = \frac{1}{3} $Parabol có đỉnh $(- \frac{b}{2a};- \frac{\Delta}{4a})=(\frac{1}{3}, 0)$ Các điểm $(0; -1), (1; -4)$ thuộc đồ thị.Đồ thị … [Đọc thêm...] vềĐề: Vẽ đồ thị hàm số $y = – 9x^2 + 6x – 1$
Bài tập Hàm số
Đề: Xét dấu của biểu thức sau: $g(x)=\frac{x^2-5x+4}{x^2-x-6}$
Đề bài: Xét dấu của biểu thức sau: $g(x)=\frac{x^2-5x+4}{x^2-x-6}$ Lời giải Giải Xét tam thức $x^2-5x+4 có \Delta_1=(-5)^2-4.1.4=9>0$Tam thức $x^2-5x+4$ có hai nghiệm là $x_1=1, x_2=4$ Tương tự $\Delta_2=(-1)^2-4.(-6)=25$Tam thức $x^2-x-6$ có hai nghiệm là $x_3=\frac{1-5}{2}=-2, x_4=\frac{1+5}{2}=3$.Ta lập bảng sau:Kết luận $g(x)>0, \forall x\in (-\infty ;-2)\cup … [Đọc thêm...] vềĐề: Xét dấu của biểu thức sau: $g(x)=\frac{x^2-5x+4}{x^2-x-6}$
Đề: Cho $n$ là một số tự nhiên $ \ge 2$ và $a > 0$. Tìm giá trị lớn nhất của tổng $\sum\limits_{i = 1}^{n – 1} x_ix_{i + 1} $Trong đó $x_i\ge 0(i = 1,2,…,n),x_1 + x_2+ … + x_n = a$
Đề bài: Cho $n$ là một số tự nhiên $ \ge 2$ và $a > 0$. Tìm giá trị lớn nhất của tổng $\sum\limits_{i = 1}^{n - 1} x_ix_{i + 1} $Trong đó $x_i\ge 0(i = 1,2,...,n),x_1 + x_2+ ... + x_n = a$ Lời giải Giả sử ${x_k} = m{\rm{ax}}\left( {{x_1},{x_2},...,{x_n}} \right)$, khi đó ta có:$\begin{array}{l}\sum\limits_{i = 1}^{n - 1} {{x_i}{x_{i + 1}} = } \sum\limits_{i = 1}^{k - 1} … [Đọc thêm...] vềĐề: Cho $n$ là một số tự nhiên $ \ge 2$ và $a > 0$. Tìm giá trị lớn nhất của tổng $\sum\limits_{i = 1}^{n – 1} x_ix_{i + 1} $Trong đó $x_i\ge 0(i = 1,2,…,n),x_1 + x_2+ … + x_n = a$
Đề: Cho hàm số $y = \frac{{u(x)}}{{v(x)}}$. Chứng minh rằng nếu $y'({x_o}) = 0$ và $v'({x_o}) \ne 0$ thì ta có$\frac{{u'({x_o})}}{{v'({x_o})}} = \frac{{u({x_o})}}{{v({x_o})}}$
Đề bài: Cho hàm số $y = \frac{{u(x)}}{{v(x)}}$. Chứng minh rằng nếu $y'({x_o}) = 0$ và $v'({x_o}) \ne 0$ thì ta có$\frac{{u'({x_o})}}{{v'({x_o})}} = \frac{{u({x_o})}}{{v({x_o})}}$ Lời giải Ta có $y' = \frac{{vu' - uv'}}{{{v^2}}}$, do đó: $y'({x_o}) = 0 \Rightarrow v({x_o})u'({x_o}) - u({x_o})v'({x_o}) = 0{\rm{ }} \Leftrightarrow … [Đọc thêm...] vềĐề: Cho hàm số $y = \frac{{u(x)}}{{v(x)}}$. Chứng minh rằng nếu $y'({x_o}) = 0$ và $v'({x_o}) \ne 0$ thì ta có$\frac{{u'({x_o})}}{{v'({x_o})}} = \frac{{u({x_o})}}{{v({x_o})}}$
Đề: Cho hàm số: $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$
Đề bài: Cho hàm số: $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$ Lời giải $1)$ Dành cho bạn đọc.$2)$ Giả sử có 2 … [Đọc thêm...] vềĐề: Cho hàm số: $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$
Đề: Tìm gia trị nhỏ nhất , giá trị lớn nhất( nếu có) của hàm số: $y=\frac{3-4x}{x^2-2x+1}$
Đề bài: Tìm gia trị nhỏ nhất , giá trị lớn nhất( nếu có) của hàm số: $y=\frac{3-4x}{x^2-2x+1}$ Lời giải Điều kiện $x\neq 1$.Ta đi tìm điều kiện của $y$ để phương trình : $\frac{3-4x}{x^2-2x+1}=y$ có nghiệm với ẩn $x$ $\Leftrightarrow f(x)=yx^2-2(y-2)x+y-3=0 (1)$Trường hợp 1: Với $y=0$ thì: $(1)\Leftrightarrow 4x-3=0\Leftrightarrow x=\frac{3}{4}$, … [Đọc thêm...] vềĐề: Tìm gia trị nhỏ nhất , giá trị lớn nhất( nếu có) của hàm số: $y=\frac{3-4x}{x^2-2x+1}$
Đề: Cho hàm số : $y=1+\cos x + \frac{ 1}{ 2} \cos 2x + \frac{ 1}{ 3} \cos 3x.$ Tìm $max y , min y.$
Đề bài: Cho hàm số : $y=1+\cos x + \frac{ 1}{ 2} \cos 2x + \frac{ 1}{ 3} \cos 3x.$ Tìm $max y , min y.$ Lời giải Tập xác định của hàm số là $R$ $y=1+\cos x + \frac{ 1}{ 2} (2 \cos ^2x -1)+\frac{ 1}{ 3} (4 \cos ^3 x -3 \cos x )$ $= \frac{ 4}{ 3} \cos ^3 x +\cos ^2 x +\frac{ 1}{ 2} $Đặt $\cos x =t,$ với mọi $x$ thì $|t| \leq 1 (A)$Hàm số có dạng $f(t) = … [Đọc thêm...] vềĐề: Cho hàm số : $y=1+\cos x + \frac{ 1}{ 2} \cos 2x + \frac{ 1}{ 3} \cos 3x.$ Tìm $max y , min y.$
Đề: Tính đạo hàm của các hàm số:$1. F(x)=\int\limits_{2x}^{x^2}\frac{t^2dx}{\sqrt{t^2+1} } $$2. G(x)=\int\limits_{\sin^2x}^{\sin x^2}(\sin t^2+\cos2t)dt $
Đề bài: Tính đạo hàm của các hàm số:$1. F(x)=\int\limits_{2x}^{x^2}\frac{t^2dx}{\sqrt{t^2+1} } $$2. G(x)=\int\limits_{\sin^2x}^{\sin x^2}(\sin t^2+\cos2t)dt $ Lời giải 1. Ta biến đổi: $F(x)=\int\limits_{2x}^{0}\frac{t^2dt}{\sqrt{t^2+1} }+\int\limits_{0}^{x^2}\frac{t^2dt}{\sqrt{t^2+1} }=-\int\limits_{0}^{2x} \frac{t^2dt}{\sqrt{t^2+1} … [Đọc thêm...] vềĐề: Tính đạo hàm của các hàm số:$1. F(x)=\int\limits_{2x}^{x^2}\frac{t^2dx}{\sqrt{t^2+1} } $$2. G(x)=\int\limits_{\sin^2x}^{\sin x^2}(\sin t^2+\cos2t)dt $
Đề: Cho hàm số: $f(x)=\left\{ \begin{array}{l} \frac{2x+3}{x+1} khi x\geq 0\\ \frac{\sqrt[3]{2+3x} }{x-2} khi -2\leq x
Đề bài: Cho hàm số: $f(x)=\left\{ \begin{array}{l} \frac{2x+3}{x+1} khi x\geq 0\\ \frac{\sqrt[3]{2+3x} }{x-2} khi -2\leq x Lời giải Nhận thấy $f(x)$ xác định trên từng khoảng xác định của nó.Khi $x=2$, thay vào công thức của $f(x)$ trên $x \in [0, +\infty)$ , ta được :$f(2)=\frac{2.2+3}{2+1}=\frac{7}{3} $Khi $x=-1$, thay vào công thức của $f(x)$ trên $x \in [-2, 0)$ , … [Đọc thêm...] vềĐề: Cho hàm số: $f(x)=\left\{ \begin{array}{l} \frac{2x+3}{x+1} khi x\geq 0\\ \frac{\sqrt[3]{2+3x} }{x-2} khi -2\leq x
Đề: Cho hàm số \(y=f(x)=\frac{x^{2}}{x^{2}+1}\) với \(x\geq 0\)Chứng minh rằng hàm số \(f(x)\) đơn điệu tăng trên khoảng \([0,+\infty]\)
Đề bài: Cho hàm số \(y=f(x)=\frac{x^{2}}{x^{2}+1}\) với \(x\geq 0\)Chứng minh rằng hàm số \(f(x)\) đơn điệu tăng trên khoảng \([0,+\infty]\) Lời giải Hàm số \(y=f(x)\) đơn điệu tăng trên \([0,+\infty)\)Ta có: \(y=f(x)=\frac{x^{2}+1-1}{x^{2}+1}=1-\frac{1}{x^{2}+1}\)Hàm số \(x^{2}+1\) đơn điệu tăng trên \([0,+\infty)\), tương tự hàm số \(-\frac{1}{x^{2}+1}\) cũng đơn điệu … [Đọc thêm...] vềĐề: Cho hàm số \(y=f(x)=\frac{x^{2}}{x^{2}+1}\) với \(x\geq 0\)Chứng minh rằng hàm số \(f(x)\) đơn điệu tăng trên khoảng \([0,+\infty]\)