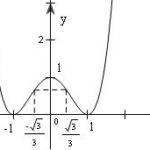
Đề bài: Cho hàm số: $y = {x^3} - mx + m - 2$, $m$ là tham số1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số khi $m = 3$.2) Dùng đồ thị $(C)$, biện luận theo $k$ số nghiệm của phương trình ${x^3} - 3x - k + 1 = 0$.3) Gọi $(Cm)$ là đồ thị của hàm số đã cho. Chứng minh rằng tiếp tuyến của $(Cm)$ tại điểm uốn của nó đi qua một điểm cố định khi $m$ thay đổi Lời giải … [Đọc thêm...] vềĐề: Cho hàm số: $y = {x^3} – mx + m – 2$, $m$ là tham số1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số khi $m = 3$.2) Dùng đồ thị $(C)$, biện luận theo $k$ số nghiệm của phương trình ${x^3} – 3x – k + 1 = 0$.3) Gọi $(Cm)$ là đồ thị của hàm số đã cho. Chứng minh rằng tiếp tuyến của $(Cm)$ tại điểm uốn của nó đi qua một điểm cố định khi $m$ thay đổi
Bài tập Hàm số
Đề: Cho hàm số $y = {x^3} + (1 – 2m){x^2} + (2 – m)x + m + 2 (C)$. Tìm $m$ để hàm số có CĐ, CT thỏa mãn $\left| {{x_1} – {x_2}} \right| > \frac{1}{3}$ , với ${x_1};{x_2}$ là hoành độ các điểm cực trị.
Đề bài: Cho hàm số $y = {x^3} + (1 - 2m){x^2} + (2 - m)x + m + 2 (C)$. Tìm $m$ để hàm số có CĐ, CT thỏa mãn $\left| {{x_1} - {x_2}} \right| > \frac{1}{3}$ , với ${x_1};{x_2}$ là hoành độ các điểm cực trị. Lời giải Ta có: \(y' = 3{x^2} + 2(1 - 2m)x + (2 - m)\) Hàm số có CĐ, CT \( \Leftrightarrow y' = 0\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = {(1 - … [Đọc thêm...] vềĐề: Cho hàm số $y = {x^3} + (1 – 2m){x^2} + (2 – m)x + m + 2 (C)$. Tìm $m$ để hàm số có CĐ, CT thỏa mãn $\left| {{x_1} – {x_2}} \right| > \frac{1}{3}$ , với ${x_1};{x_2}$ là hoành độ các điểm cực trị.
Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = cos^4x + sin^4x + sinxcos x + 1$
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = cos^4x + sin^4x + sinxcos x + 1$ Lời giải $y =\ cos^4x + \sin^4x + \sin x\cos x + 1=-\frac{1}{2} \sin^22x+\frac{1}{2} \sin2x+2$ Đặt $\sin2x=t(|t|\leq 1)\Rightarrow y=-\frac{1}{2} t^2+\frac{1}{2} t+2$ là parabol quay bề lõm xuống dưới, hoành độ đỉnh $t_1=\frac{1}{2} \in [-1,1]$Vậy $\max y=-\frac{1}{2} … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = cos^4x + sin^4x + sinxcos x + 1$
Đề: Cho hàm số: $y = \frac{{{x^2}cos\alpha – 2x + cos\alpha }}{{{x^2} – 2xcos \alpha + 1}}$Với tham số $\alpha \in (0; \pi)$. Chứng minh rằng với mọi giá trị của $x$, ta đều có $ – 1 \le y \le 1$
Đề bài: Cho hàm số: $y = \frac{{{x^2}cos\alpha - 2x + cos\alpha }}{{{x^2} - 2xcos \alpha + 1}}$Với tham số $\alpha \in (0; \pi)$. Chứng minh rằng với mọi giá trị của $x$, ta đều có $ - 1 \le y \le 1$ Lời giải Ta có: $y = \frac{{{x^2}c{\rm{os}}\alpha - 2x + c{\rm{os}}\alpha }}{{{{\left( {x - c{\rm{os}}\alpha } \right)}^2} + {{\sin }^2}\alpha }}$Do $\alpha \in (0{\rm{ … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{{x^2}cos\alpha – 2x + cos\alpha }}{{{x^2} – 2xcos \alpha + 1}}$Với tham số $\alpha \in (0; \pi)$. Chứng minh rằng với mọi giá trị của $x$, ta đều có $ – 1 \le y \le 1$
Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:$f(x)=\sin x\cos^2x$ với $0\leq x\leq \frac{\pi}{2}$.
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:$f(x)=\sin x\cos^2x$ với $0\leq x\leq \frac{\pi}{2}$. Lời giải Cần lời giải chi tiết. (đáp số: $\frac{3\sqrt{3}}{16}$). … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:$f(x)=\sin x\cos^2x$ với $0\leq x\leq \frac{\pi}{2}$.
Đề: Xác định $m$ để các hàm số sau có tập xác định là $R$a) $f(x)=\sqrt{(m-2)x^2+(m-2)x+4}$ b) $g(x)=\frac{x^2+mx-m}{x^2-2mx+m+2}$
Đề bài: Xác định $m$ để các hàm số sau có tập xác định là $R$a) $f(x)=\sqrt{(m-2)x^2+(m-2)x+4}$ b) $g(x)=\frac{x^2+mx-m}{x^2-2mx+m+2}$ Lời giải Giảia) Hàm số có tập xác định $R$ khi và chỉ khi $(m-2)x^2+(m-2)x+4\geq 0$ với mọi $x\in R$ (*) * Xét $m=2:$ (*) trở thành $4\geq 0$ ( đúng).Vậy $m=2$ thỏa mãn yêu cầu bài toán * Xét $m\neq 2$: Ta có … [Đọc thêm...] vềĐề: Xác định $m$ để các hàm số sau có tập xác định là $R$a) $f(x)=\sqrt{(m-2)x^2+(m-2)x+4}$ b) $g(x)=\frac{x^2+mx-m}{x^2-2mx+m+2}$
Đề: Xác định $m$ để đồ thị hàm số $(C):y=x^{4}+4mx^{3}-2x^{2}-12mx$ có trục đối xứng song song với $Oy$.
Đề bài: Xác định $m$ để đồ thị hàm số $(C):y=x^{4}+4mx^{3}-2x^{2}-12mx$ có trục đối xứng song song với $Oy$. Lời giải Giả sử đồ thị có trục đối xứng song song với $Oy$ là $x=a(a\neq 0)$Khi đó,với phép biến đổi tọa độ:$\begin{cases} X=x-a \\Y=y\end{cases} \Leftrightarrow \begin{cases} x=X+a \\y=Y \end{cases} $Hàm số $Y=(X+a)^{4}+4m(X+a)^{3}-2(X+a)^{2}-12m(X+a)$ là hàm số … [Đọc thêm...] vềĐề: Xác định $m$ để đồ thị hàm số $(C):y=x^{4}+4mx^{3}-2x^{2}-12mx$ có trục đối xứng song song với $Oy$.
Đề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}{x^2} + 5x + 4 < 0\\{x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.$
Đề bài: Giải hệ bất phương trình: $\left\{ \begin{array}{l}{x^2} + 5x + 4 < 0\\{x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.$ Lời giải Giải hệ : $\left\{ \begin{array}{l}{x^2} + 5x + 4 {x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.\Leftrightarrow \begin{cases}-40 \end{cases} $Xét hàm $f(x)=x^3+3x^2-9x-10, x\in (-4;-1)$$f'(x)=3x^2+6x-9, f'(x)=0\Leftrightarrow x=-3, … [Đọc thêm...] vềĐề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}{x^2} + 5x + 4 < 0\\{x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.$
Đề: $1$. Giải phương trình: $x^4 – 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 – 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 – 2x^2 + 1- m = 0$
Đề bài: $1$. Giải phương trình: $x^4 - 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 - 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 - 2x^2 + 1- m = 0$ Lời giải $1.$ Ta có $x^4-2x^2+1=(x^2-1)^2=0\Leftrightarrow x=\pm1$$2.$ Khảo sát hàm số: xin dành cho bạn đọc, đồ thị hàm số như hình vẽ:$3.$ Nghiệm phương trình là hoành độ giao diểm của hai … [Đọc thêm...] vềĐề: $1$. Giải phương trình: $x^4 – 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 – 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 – 2x^2 + 1- m = 0$
Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = {5^{x – 1}} + {5^{ – x – 1}}$
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = {5^{x - 1}} + {5^{ - x - 1}}$ Lời giải GiảiTa có:${y^ / } = \left( {{5^{x - 1}} - {5^{ - x - 1}}} \right)\ln 5$ Bảng biến thiên : Vậy : Không có giá trị lớn nhất., khi $x = 0$ … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = {5^{x – 1}} + {5^{ – x – 1}}$