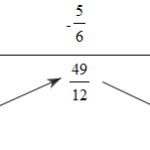
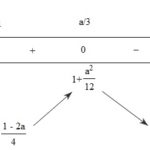
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(y = \frac{{3{x^2} + 10x + 20}}{{{x^2} + 2x + 3}}\) Lời giải \(y = \frac{{3{x^2} + 10x + 20}}{{{x^2} + 2x + 3}} \Leftrightarrow \left( {y - 3} \right){x^2} + \left( {2y - 10} \right)x + 3y - 20 = 0\)\(\Delta ' = {\left( {y - 5} \right)^2} - \left( {y - 3} \right)\left( {3y - 20} \right) \ge 0\)\( \Leftrightarrow … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(y = \frac{{3{x^2} + 10x + 20}}{{{x^2} + 2x + 3}}\)
Bài tập Hàm số
Đề: Cho hàm số f(x) xác định trên R thỏa mãn điều kiện${(f(x) – f(y))^2} \le |x-y|^3 \forall x,y \in R$ (1)Chứng minh rằng $f(x)$ có đạo hàm trên $R$ và $f(x) = C$, trong đó $C$ là một hằng số
Đề bài: Cho hàm số f(x) xác định trên R thỏa mãn điều kiện${(f(x) - f(y))^2} \le |x-y|^3 \forall x,y \in R$ (1)Chứng minh rằng $f(x)$ có đạo hàm trên $R$ và $f(x) = C$, trong đó $C$ là một hằng số Lời giải Từ $(1)$ với $x \ne y$ ta có: $\left| {\frac{{f(x) - f(y)}}{{x - y}}} \right| \le {\left| {x - y} \right|^{1/2}}$$ \Rightarrow \mathop {\lim … [Đọc thêm...] vềĐề: Cho hàm số f(x) xác định trên R thỏa mãn điều kiện${(f(x) – f(y))^2} \le |x-y|^3 \forall x,y \in R$ (1)Chứng minh rằng $f(x)$ có đạo hàm trên $R$ và $f(x) = C$, trong đó $C$ là một hằng số
Đề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $A = \frac{{{x^2} + {y^2}}}{{{x^2} + xy + 4{y^2}}}$Trong đó $x, y$ là các số thực tùy ý không đồng thời bằng không.
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $A = \frac{{{x^2} + {y^2}}}{{{x^2} + xy + 4{y^2}}}$Trong đó $x, y$ là các số thực tùy ý không đồng thời bằng không. Lời giải Dễ nhận thấy rằng $A$ luôn xác định với $\forall x,y \in R$ không đồng thời bằng $0$.a) Xét $x = 0$, khi đó $A = \frac{{{y^2}}}{{4{y^2}}} = \frac{1}{4} \left( {\forall y \in … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $A = \frac{{{x^2} + {y^2}}}{{{x^2} + xy + 4{y^2}}}$Trong đó $x, y$ là các số thực tùy ý không đồng thời bằng không.
Đề: Tìm đạo hàm của hàm số $y=\frac{ax^{2}+bx+c}{dx+e}$
Đề bài: Tìm đạo hàm của hàm số $y=\frac{ax^{2}+bx+c}{dx+e}$ Lời giải $y=\frac{ax^{2}+bx+c}{dx+e}$ $ \Leftrightarrow y^{'}=\frac{(ax^{2}+bx+c)^{'}(dx+e)-(ax^{2}+bx+c)(dx+e)^{'}}{(dx+e)^{2}}$ $=\frac{(2ax+b)(dx+e)-(ax^{2}+bx+c)d}{(dx+e)^{2}}$ $=\frac{adx^{2}+2aex+be-cd}{(dx+e)^{2}}$ Vậy $(\frac{ax^{2}+bx+c}{dx+e})^{'}=\frac{adx^{2}+2aex+be-cd}{(dx+e)^{2}}$ … [Đọc thêm...] vềĐề: Tìm đạo hàm của hàm số $y=\frac{ax^{2}+bx+c}{dx+e}$
Đề: Cho các số thực dương $x,y,z$ thỏa mãn $xy+yz+zx =\frac{9}{4} (1)$Tìm $\min Q$, với $Q=x^2+14y^2+10z^2-4\sqrt{2y}$
Đề bài: Cho các số thực dương $x,y,z$ thỏa mãn $xy+yz+zx =\frac{9}{4} (1)$Tìm $\min Q$, với $Q=x^2+14y^2+10z^2-4\sqrt{2y}$ Lời giải Theo Cô-si ta có $\frac{x^2}{2}+8z^2 \geq 4xz; \frac{x^2}{2}+8y^2 \geq 4yz; 2(y^2+z^2) \geq 4xy$Công thức từng vế các bất đẳng thức trên ta có: $x^2+10y^2+10z^2 \geq 4(xy+yz+zx)$* Kết hợp với $(1)$ suy ra $x^2+10y^2+10z^2 \geq … [Đọc thêm...] vềĐề: Cho các số thực dương $x,y,z$ thỏa mãn $xy+yz+zx =\frac{9}{4} (1)$Tìm $\min Q$, với $Q=x^2+14y^2+10z^2-4\sqrt{2y}$
Đề: Cho hàm số $y= ax^2 + bx + c$.a) Xác định $a, b, c$ biết hàm số đi qua các điểm $A(0;2), B(1;-6), C(-1;4)$.b) Khảo sát và vẽ đồ thị hàm số vừa tìm được.
Đề bài: Cho hàm số $y= ax^2 + bx + c$.a) Xác định $a, b, c$ biết hàm số đi qua các điểm $A(0;2), B(1;-6), C(-1;4)$.b) Khảo sát và vẽ đồ thị hàm số vừa tìm được. Lời giải a) Giải hệ phương trình ba ẩn $a, b, c$ ta được :$\begin{cases}a.0+b.0+c=2 \\ a.1+b.1+c=-6 \\a.1-b.1+c=4 \end{cases}\Leftrightarrow \begin{cases}a=-3 \\ b=-5\\c=2 \end{cases}$ và $y = -3x^2 - 5x+2$.b) Bảng … [Đọc thêm...] vềĐề: Cho hàm số $y= ax^2 + bx + c$.a) Xác định $a, b, c$ biết hàm số đi qua các điểm $A(0;2), B(1;-6), C(-1;4)$.b) Khảo sát và vẽ đồ thị hàm số vừa tìm được.
Đề: Tìm tất cả các cặp số dương $(x, y)$sao cho biểu thức: $f(x,y) = \frac{x^4}{y^4} + \frac{y^4}{x^4} -( {\frac{x^2}{y^2} + \frac{y^2}{x^2}} ) + \frac{x}{y} + \frac{y}{x}$ đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó
Đề bài: Tìm tất cả các cặp số dương $(x, y)$sao cho biểu thức: $f(x,y) = \frac{x^4}{y^4} + \frac{y^4}{x^4} -( {\frac{x^2}{y^2} + \frac{y^2}{x^2}} ) + \frac{x}{y} + \frac{y}{x}$ đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó Lời giải Cách 1. Ta có$f(x,y) = {\left( {\frac{{{x^2}}}{{{y^2}}} - 1} \right)^2} + {\left( {\frac{{{y^2}}}{{{x^2}}} - 1} \right)^2} + {\left( … [Đọc thêm...] vềĐề: Tìm tất cả các cặp số dương $(x, y)$sao cho biểu thức: $f(x,y) = \frac{x^4}{y^4} + \frac{y^4}{x^4} -( {\frac{x^2}{y^2} + \frac{y^2}{x^2}} ) + \frac{x}{y} + \frac{y}{x}$ đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó
Đề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = \frac{{{x^2} – 6x + 5}}{{2x – 1}}\)$2$. Biện luận số nghiệm của phương trình \({x^2} – 6x + 5 = k|2x – 1|\) theo tham số $k$.
Đề bài: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = \frac{{{x^2} - 6x + 5}}{{2x - 1}}\)$2$. Biện luận số nghiệm của phương trình \({x^2} - 6x + 5 = k|2x - 1|\) theo tham số $k$. Lời giải $1$. Bạn đọc tự giải:$2$. \(PT \Leftrightarrow \frac{{{x^2} - 6x + 5}}{{|2x - 1|}} = k\) Số nghiệm phương trình bằng số giao điểm đường thẳng $y = k$ với đồ thị … [Đọc thêm...] vềĐề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = \frac{{{x^2} – 6x + 5}}{{2x – 1}}\)$2$. Biện luận số nghiệm của phương trình \({x^2} – 6x + 5 = k|2x – 1|\) theo tham số $k$.
Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y=sin^{6}x+cos^{6}x+asinxcosx$
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y=sin^{6}x+cos^{6}x+asinxcosx$ Lời giải \(y = {\sin ^6}x + c{\rm{o}}{{\rm{s}}^6}x + {\rm{a}}\sin x\cos x =- \frac{3}{4}{\sin ^2}2x + \frac{a}{2}\sin 2x + 1\)Đặt \(t = \sin 2x\left( { - 1 \le t \le 1} \right)\), khi đó:\(y = f\left( t \right) = - \frac{3}{4}{t^2} + \frac{a}{2}t + 1\,\,\,\left( {t \in \left[ { - 1,\,1} … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y=sin^{6}x+cos^{6}x+asinxcosx$
Đề: Chứng minh rằng phương trình $x^{3}+3x^{2}+5x-1=0$ có ít nhất một nghiệm trên khoảng $(0,1)$
Đề bài: Chứng minh rằng phương trình $x^{3}+3x^{2}+5x-1=0$ có ít nhất một nghiệm trên khoảng $(0,1)$ Lời giải Xét hàm số $f(x)=x^{3}+3x^{2}+5x-1$$f(x)$ là hàm đa thức nên liên tục trên đoạn $[0,1]$Mặt khác: $\begin{cases}f(0)=-1 \\ f(1)=8 \end{cases}$$\Rightarrow f(0).f(1)=-8Vậy phương trình $f(x)=0$ có ít nhất một nghiệm trên khoảng $(0,1)$ … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình $x^{3}+3x^{2}+5x-1=0$ có ít nhất một nghiệm trên khoảng $(0,1)$