Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Bài tập Hàm số

Đề: Tìm tập xác định của hàm số: $y=\frac{\tan x+\cot x}{\cos 2x}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm tập xác định của hàm số: $y=\frac{\tan x+\cot x}{\cos 2x}$ Lời giải \( \tan x \) xác định với \( x\in D_{1}=\left \{ \right.x\in R/x\neq \frac{\pi}{2}+k\pi,k\in Z\left. \right \} \). \( \cot x \) xác định với \( x \in D_{2}=\left \{ \right.x\in R/x\neq k\pi\left.\right \} \). \( \frac{1}{\cos 2x} \) xác định với \( x \) sao cho \( \cos 2x\neq 0 \), nghĩa là … [Đọc thêm...] vềĐề: Tìm tập xác định của hàm số: $y=\frac{\tan x+\cot x}{\cos 2x}$

Đề: Tìm đạo hàm của các hàm số:a) \(y=\cos^{3}(x^{2}+1)\)b) \(y=\cot (3x^{2}+\frac{x}{2})\).

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm đạo hàm của các hàm số:a) \(y=\cos^{3}(x^{2}+1)\)b) \(y=\cot (3x^{2}+\frac{x}{2})\). Lời giải a) \(y'=[\cos^{3}(x^{2}+1)]'=3\cos^{2}(x^{2}+1).[\cos (x^{2}+1)]'\)\(=-3\cos^{2}(x^{2}+1).\sin (x^{2}+1).[x^{2}+1]'\)\(=-6x\cos^{2}(x^{2}+1).\sin (x^{2}+1)\)b) \(y'=[\cot (3x^{2}+\frac{x}{2})]'=-\frac{(3x^{2}+\frac{x}{2})'}{\sin … [Đọc thêm...] vềĐề: Tìm đạo hàm của các hàm số:a) \(y=\cos^{3}(x^{2}+1)\)b) \(y=\cot (3x^{2}+\frac{x}{2})\).

Đề: Cho đồ thị $(C)$ của hàm số $y = \frac{2x – 1}{x – 1}$. Viết phương trình tiếp tuyến của $(C)$, biết khoảng cách từ điểm $I(1;2)$ đến tiếp tuyến bằng $ \sqrt {2} $

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho đồ thị $(C)$ của hàm số $y = \frac{2x - 1}{x - 1}$. Viết phương trình tiếp tuyến của $(C)$, biết khoảng cách từ điểm $I(1;2)$ đến tiếp tuyến bằng $ \sqrt {2} $ Lời giải Tiếp tuyến của (C) tại điểm $M({x_0};f({x_0})) \in (C)$  có phương trình  $ y = f'({x_0})(x - {x_0}) + f({x_0}) $ Hay   $x + {({x_0} - 1)^2}y - 2{x_0}^2 + 2{x_0} - 1 = 0$  (*) Khoảng cách từ … [Đọc thêm...] vềĐề: Cho đồ thị $(C)$ của hàm số $y = \frac{2x – 1}{x – 1}$. Viết phương trình tiếp tuyến của $(C)$, biết khoảng cách từ điểm $I(1;2)$ đến tiếp tuyến bằng $ \sqrt {2} $

Đề: Cho hàm số  $y = {x^3} – 3a{x^2} + 4{a^3}$.1) Với $a > 0$ cố định, hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Xác định $a$ để các điểm cực đại và cực tiểu của đồ thị là đối xứng với nhau qua đường thẳng $y = x$.3) Xác định $a$ để đường thẳng $y = x$ cắt đồ thị tại 3 điểm phân biệt $A, B, C$ với $AB = BC$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số  $y = {x^3} - 3a{x^2} + 4{a^3}$.1) Với $a > 0$ cố định, hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Xác định $a$ để các điểm cực đại và cực tiểu của đồ thị là đối xứng với nhau qua đường thẳng $y = x$.3) Xác định $a$ để đường thẳng $y = x$ cắt đồ thị tại 3 điểm phân biệt $A, B, C$ với $AB = BC$ Lời giải $1)$ Dành cho bạn đọc.$2)$ Ta có $y' = … [Đọc thêm...] vềĐề: Cho hàm số  $y = {x^3} – 3a{x^2} + 4{a^3}$.1) Với $a > 0$ cố định, hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Xác định $a$ để các điểm cực đại và cực tiểu của đồ thị là đối xứng với nhau qua đường thẳng $y = x$.3) Xác định $a$ để đường thẳng $y = x$ cắt đồ thị tại 3 điểm phân biệt $A, B, C$ với $AB = BC$

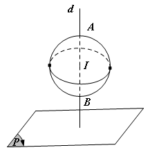
Đề: Tìm điểm $A$ trên mặt cầu $(S): x^2+y^2+z^2-2x+2z-2=0$ sao cho khoảng cách từ $A$ đến mặt phẳng $(P): 2x-2y+z+6=0$ là lớn nhất, nhỏ nhất.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm điểm $A$ trên mặt cầu $(S): x^2+y^2+z^2-2x+2z-2=0$ sao cho khoảng cách từ $A$ đến mặt phẳng $(P): 2x-2y+z+6=0$ là lớn nhất, nhỏ nhất. Lời giải Đưa $(S)$ về dạng: $(x-1)^2+y^2+(z+1)^2=4$.Vậy $(S)$ là mặt cầu tâm tại $I(1;0;-1)$ và bán kính $R=2$.Đường thẳng $(d)$ qua $I$ nhận vectơ pháp tuyến $\overrightarrow{n}=(2;-2;1)$ của $(P)$ là vectơ chỉ phương nên có … [Đọc thêm...] vềĐề: Tìm điểm $A$ trên mặt cầu $(S): x^2+y^2+z^2-2x+2z-2=0$ sao cho khoảng cách từ $A$ đến mặt phẳng $(P): 2x-2y+z+6=0$ là lớn nhất, nhỏ nhất.

Đề: Tìm đạo hàm của các hàm số:a) \(y=\frac{x^{3}-2x}{x^{2}+x+1}\)b) \(y=\frac{2x^{4}}{9-x^{2}}\).

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm đạo hàm của các hàm số:a) \(y=\frac{x^{3}-2x}{x^{2}+x+1}\)b) \(y=\frac{2x^{4}}{9-x^{2}}\). Lời giải a) Ta có: \(y'=\frac{(x^{3}-2x)'(x^{2}+x+1)-(x^{3}-2x)(x^{2}+x+1)'}{(x^{2}+x+1)^{2}}\)\(=\frac{(3x^{2}-2)(x^{2}+x+1)-(x^{3}-2x)(2x+1)}{(x^{2}+x+1)^{2}}=\frac{x^{4}+2x^{3}+5x^{2}-2}{(x^{2}+x+1)^{2}}\).b) Làm tương tự câu a): … [Đọc thêm...] vềĐề: Tìm đạo hàm của các hàm số:a) \(y=\frac{x^{3}-2x}{x^{2}+x+1}\)b) \(y=\frac{2x^{4}}{9-x^{2}}\).

Đề: Chứng minh rằng phương trình:   $ 5x^4+40x^3+105x^2+100x+24 = 0 $ có bốn nghiệm âm phân biệt.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Chứng minh rằng phương trình:   $ 5x^4+40x^3+105x^2+100x+24 = 0 $ có bốn nghiệm âm phân biệt. Lời giải Xét hàm số $f(x)=5x^4+40x^3+105x^2+100x+24$$f(x)$ liên tục trên $R$.Ta có: $f(-4)=24, f(-3)=-6, f(-2)=4, f(-1)=-6, f(0)=24$$f(-4).f(-3)=-144$f(-3).f(-2)=-24$f(-2).f(-1)=-24$f(-1).f(0)=-144Các khoảng $(-4;-3); (-3;-2); … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình:   $ 5x^4+40x^3+105x^2+100x+24 = 0 $ có bốn nghiệm âm phân biệt.

Đề: Tìm giá trị lớn nhất của biểu thức:$A=\sqrt{a+\cos x}+\sqrt{a+\sin x}$ với $x\in R,a\geq 1$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm giá trị lớn nhất của biểu thức:$A=\sqrt{a+\cos x}+\sqrt{a+\sin x}$ với $x\in R,a\geq 1$ Lời giải Trong mặt phẳng tọa độ $Oxy$ chọn:$\overrightarrow {u}=(1;1) \Rightarrow |\overrightarrow {u}|=\sqrt{2}$$\overrightarrow {v}=(\sqrt{a+\cos x};\sqrt{a+\sin x}) \Rightarrow |\overrightarrow {v}|=\sqrt{2a+\sqrt{2}\sin (x+\frac{\pi}{4})}$$A=\overrightarrow … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất của biểu thức:$A=\sqrt{a+\cos x}+\sqrt{a+\sin x}$ với $x\in R,a\geq 1$

Đề: Cho hàm số $y=\frac{x+2}{2x+3} (1)$. Viết phương trình tiếp tuyến của đồ thị hàm số $(1)$, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt $A, B$ và tam giác $OAB$ cân tại gốc tọa độ $O$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số $y=\frac{x+2}{2x+3} (1)$. Viết phương trình tiếp tuyến của đồ thị hàm số $(1)$, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt $A, B$ và tam giác $OAB$ cân tại gốc tọa độ $O$ Lời giải Tam giác $OAB$ vuông cân tại $O$, suy ra hệ số góc tiếp tuyến bằng $\pm 1$. Gọi tọa độ tiếp điểm là $(x_0;y_0)$ ta có: … [Đọc thêm...] vềĐề: Cho hàm số $y=\frac{x+2}{2x+3} (1)$. Viết phương trình tiếp tuyến của đồ thị hàm số $(1)$, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt $A, B$ và tam giác $OAB$ cân tại gốc tọa độ $O$

Đề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số : $y=2\sin2x(\sin2x-4\cos2x)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số : $y=2\sin2x(\sin2x-4\cos2x)$ Lời giải Ta có:        $y=2\sin2x(\sin2x-4\cos2x)=2\sin^22x-8\sin2x\cos2x$         $=1-\cos 4x-4\sin 4x=1-\sqrt{17} ( \frac{4}{\sqrt{17} }\sin 4x+\frac{1}{\sqrt{17} }\cos 4x)   $         $=1-\sqrt{17}\sin (4x+\alpha) $Suy ra:+) Min $y=1-\sqrt{17} $ đạt được khi:         $\sin … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số : $y=2\sin2x(\sin2x-4\cos2x)$