Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y=sin^{6}x+cos^{6}x+asinxcosx$

Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y=sin^{6}x+cos^{6}x+asinxcosx$

Lời giải

\(y = {\sin ^6}x + c{\rm{o}}{{\rm{s}}^6}x + {\rm{a}}\sin x\cos x =- \frac{3}{4}{\sin ^2}2x + \frac{a}{2}\sin 2x + 1\)

Đặt \(t = \sin 2x\left( { – 1 \le t \le 1} \right)\), khi đó:
\(y = f\left( t \right) =  – \frac{3}{4}{t^2} + \frac{a}{2}t + 1\,\,\,\left( {t \in \left[ { – 1,\,1} \right]} \right)\)

\(\Rightarrow f’\left( t \right) =  – \frac{3}{2}t + \frac{a}{2}\,\,\\\,f’\left( t \right) = 0 \Leftrightarrow t = \frac{a}{3}\)

Nếu \(\frac{a}{3} \le -1     \left( {a \le- 3} \right)\) thì $f(t)$ nghịch biến trong \(\left[ { – 1,\,1} \right]\)

\( \Rightarrow \max f = f\left( { – 1} \right) = \frac{{1 – 2a}}{4};\,\,\min \,f = f\left( 1 \right) = \frac{{1 + 2a}}{4}\)

Nếu \(\frac{a}{3} \ge 1     \left( {a \ge 3} \right)\) thì $f(t)$ đồng biến trong \(\left[ { – 1,\,1} \right]\)

\( \Rightarrow \max f = f\left( 1 \right) = \frac{{1 + 2a}}{4};\,\,\min \,f = f\left( { – 1} \right) = \frac{{1 – 2a}}{4}\)

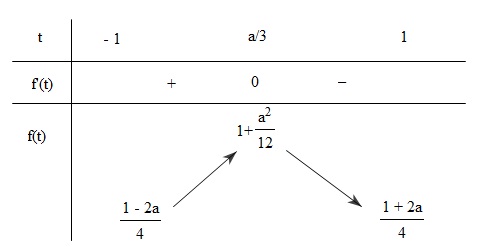
Nếu \( – 1
Ta có bảng biến thiên:

Nên \(m{\rm{ax}}\,f = 1 + \frac{{{a^2}}}{{12}};\,\,\min \,f = \frac{{1 – 2|a|}}{4}\)

Kết luận \(\min y = \dfrac{{1 – 2|a|}}{4};\,\,\max y = \left\{ \begin{array}{l}
\dfrac{{1 + 2|a|}}{4}\,\,\,khi\,|a| \ge 3\\
1 + \dfrac{{{a^2}}}{{12}}\,\,\,khi\,|a| \end{array} \right.\)