Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

TN THPT 2021

[CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG-2020] Cho \(f(x)\) là hàm đa thức bậc \(6\) sao cho đồ thị hàm số \(y = f'(x)\) như hình vẽ

Ngày Thuộc chủ đề:Blog, Trắc nghiệm Cực trị của hàm số Tag với:, ,

PHƯƠNG PHÁP GHÉP TRỤC TRONG BÀI TOÁN HÀM HỢP Câu hỏi: [CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG-2020] Cho \(f(x)\) là hàm đa thức bậc \(6\) sao cho đồ thị hàm số \(y = f'(x)\) như hình vẽ Tìm số điểm cực trị của hàm số \(y = g(x) = f\left( {{x^2} + 4x + 5} \right)\). A. \(2\). B. \(5\). C. \(3\). D. \(1\). Lời giải Chọn C Cách 2: PP tự … [Đọc thêm...] về[CHUYÊN NGUYỄN TRÃI HẢI DƯƠNG-2020] Cho \(f(x)\) là hàm đa thức bậc \(6\) sao cho đồ thị hàm số \(y = f'(x)\) như hình vẽ

MH-BGD-L1: Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2}} \right)\) là

Ngày Thuộc chủ đề:Blog, Trắc nghiệm Cực trị của hàm số Tag với:, ,

PHƯƠNG PHÁP GHÉP TRỤC TRONG BÀI TOÁN HÀM HỢP Câu hỏi: MH-BGD-L1: Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2}} \right)\) là A. \(5\). B. \(3\). C. \(7\). D. \(11\). Lời giải Chọn C Cách 1: Tự luận truyền thống Từ đồ thị ta có … [Đọc thêm...] vềMH-BGD-L1: Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2}} \right)\) là

[CHUYÊN KHTN HÀ NỘI LẦN 3-2020] Cho hàm số \(y = f\left( x \right)\).Hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ.

Ngày Thuộc chủ đề:Blog, Trắc nghiệm Cực trị của hàm số Tag với:, ,

PHƯƠNG PHÁP GHÉP TRỤC TRONG BÀI TOÁN HÀM HỢP Câu hỏi: [CHUYÊN KHTN HÀ NỘI LẦN 3-2020] Cho hàm số \(y = f\left( x \right)\).Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(y = f\left( {{x^2} - 1} \right)\) có bao nhiêu điểm cực trị? A. \(5\). B. \(7\). C. \(4\). D. \(3\). Lời giải Chọn A Cách 1: Tự luận … [Đọc thêm...] về [CHUYÊN KHTN HÀ NỘI LẦN 3-2020] Cho hàm số \(y = f\left( x \right)\).Hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ.

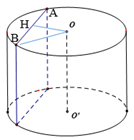
Cắt hình trụ \((T)\) bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(2a\), ta được thiết diện là một hình vuông có diện tích bẳng \(16{a^2}\). Diện tích xung quanh của \((T)\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm mặt Trụ Tag với:,

Cắt hình trụ \((T)\) bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(2a\), ta được thiết diện là một hình vuông có diện tích bẳng \(16{a^2}\). Diện tích xung quanh của \((T)\) bằng A. \(\frac{{16\sqrt 2 }}{3}\pi … [Đọc thêm...] vềCắt hình trụ \((T)\) bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(2a\), ta được thiết diện là một hình vuông có diện tích bẳng \(16{a^2}\). Diện tích xung quanh của \((T)\) bằng

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(y = f’\left( x \right) = (x – 5)({x^2} – 4),x \in R\). Có bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { – 100;100} \right]\) để hàm số\(y = g(x) = f\left( {\left| {{x^3} + 3x} \right| + m} \right)\) có ít nhất 3 điểm cực trị?

Ngày Thuộc chủ đề:Blog, Trắc nghiệm Cực trị của hàm số Tag với:,

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(y = f'\left( x \right) = (x - 5)({x^2} - 4),x \in R\). Có bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { - 100;100} \right]\) để hàm số\(y = g(x) = f\left( {\left| {{x^3} + 3x} \right| + m} \right)\) có ít nhất 3 điểm cực trị? A. \(105\). B. \(106\). C. \(104\). D. \(103\). LỜI GIẢI CHI TIẾT … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm \(y = f’\left( x \right) = (x – 5)({x^2} – 4),x \in R\). Có bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { – 100;100} \right]\) để hàm số\(y = g(x) = f\left( {\left| {{x^3} + 3x} \right| + m} \right)\) có ít nhất 3 điểm cực trị?

Cho hai số \(x,\,y\) thỏa mãn \(x + y > 0\) và \({10^{{x^2} + {y^2}}} + {2021^{2021}}.\log \frac{{{x^2} + {y^2}}}{{x + y}} \le {100^{x + y}} + {2021^{2021}}.\log 2\).

Tìm tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {x^2} + {y^2} – 10x – 2y + 2.\)

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:,

Câu hỏi: Cho hai số \(x,\,y\) thỏa mãn \(x + y > 0\) và \({10^{{x^2} + {y^2}}} + {2021^{2021}}.\log \frac{{{x^2} + {y^2}}}{{x + y}} \le {100^{x + y}} + {2021^{2021}}.\log 2\). Tìm tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {x^2} + {y^2} - 10x - 2y + 2.\) A. \( - 12\). B. \( - 8\). C. \( - 6 - 8\sqrt 2 .\) D. \(8\sqrt 2 - 6.\) LỜI … [Đọc thêm...] vềCho hai số \(x,\,y\) thỏa mãn \(x + y > 0\) và \({10^{{x^2} + {y^2}}} + {2021^{2021}}.\log \frac{{{x^2} + {y^2}}}{{x + y}} \le {100^{x + y}} + {2021^{2021}}.\log 2\).

Tìm tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {x^2} + {y^2} – 10x – 2y + 2.\)

Trong không gian , cho hai điểm \(A\left( {3; – 2;2} \right)\), \(B\left( { – 2;2;0} \right)\) và mặt phẳng \(\left( P \right):2x – y + 2z – 3 = 0\). Xét các điểm \(M\), \(N\) di động trên \(\left( P \right)\) sao cho \(MN = 1\). Giá trị nhỏ nhất của \(2M{A^2} + 3N{B^2}\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Xác định điểm thỏa điều kiện cho trước Tag với:,

Câu hỏi: Trong không gian , cho hai điểm \(A\left( {3; - 2;2} \right)\), \(B\left( { - 2;2;0} \right)\) và mặt phẳng \(\left( P \right):2x - y + 2z - 3 = 0\). Xét các điểm \(M\), \(N\) di động trên \(\left( P \right)\) sao cho \(MN = 1\). Giá trị nhỏ nhất của \(2M{A^2} + 3N{B^2}\) bằng A. \(49,8\). B. \(45\). C. \(53\). D. \(55,8\). LỜI GIẢI CHI TIẾT Gọi … [Đọc thêm...] vềTrong không gian , cho hai điểm \(A\left( {3; – 2;2} \right)\), \(B\left( { – 2;2;0} \right)\) và mặt phẳng \(\left( P \right):2x – y + 2z – 3 = 0\). Xét các điểm \(M\), \(N\) di động trên \(\left( P \right)\) sao cho \(MN = 1\). Giá trị nhỏ nhất của \(2M{A^2} + 3N{B^2}\) bằng

Cho hàm số \(f\left( x \right) = {x^{2021}} + 2021x\). Gọi \({m_0}\)là số lớn nhất trong các số nguyên \(m\)thỏa mãn \(f\left( {m – 2020} \right) + f\left( {2021m – {5^8}} \right) \le 0\). Mệnh đề nào sau đây đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Nguyên hàm Tag với:,

Câu hỏi: Cho hàm số \(f\left( x \right) = {x^{2021}} + 2021x\). Gọi \({m_0}\)là số lớn nhất trong các số nguyên \(m\)thỏa mãn \(f\left( {m - 2020} \right) + f\left( {2021m - {5^8}} \right) \le 0\). Mệnh đề nào sau đây đúng? A. \({m_0} \in \left[ {180;\,191} \right]\). B. \({m_0} \in \left( {191;\,204} \right]\). C. \({m_0} \in \left( {204;223} \right)\). D. … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^{2021}} + 2021x\). Gọi \({m_0}\)là số lớn nhất trong các số nguyên \(m\)thỏa mãn \(f\left( {m – 2020} \right) + f\left( {2021m – {5^8}} \right) \le 0\). Mệnh đề nào sau đây đúng?

Cho \(f\left( x \right) = \left\{ \begin{array}{l}4x + 1\,\,\,\,\,\,\,\,\,\,khi\,x \ge 1\\3{x^2} + 2\,\,\,\,\,\,\,\,\,khi\,x < 1\end{array} \right.\). Giả sử \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 0 \right) = 2\). Giá trị của \(F\left( { – 2} \right) + 3F\left( 4 \right)\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Nguyên hàm Tag với:,

Câu hỏi: Cho \(f\left( x \right) = \left\{ \begin{array}{l}4x + 1\,\,\,\,\,\,\,\,\,\,khi\,x \ge 1\\3{x^2} + 2\,\,\,\,\,\,\,\,\,khi\,x < 1\end{array} \right.\). Giả sử \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 0 \right) = 2\). Giá trị của \(F\left( { - 2} \right) + 3F\left( 4 \right)\) bằng A. \(38\). B. \( - … [Đọc thêm...] vềCho \(f\left( x \right) = \left\{ \begin{array}{l}4x + 1\,\,\,\,\,\,\,\,\,\,khi\,x \ge 1\\3{x^2} + 2\,\,\,\,\,\,\,\,\,khi\,x < 1\end{array} \right.\). Giả sử \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 0 \right) = 2\). Giá trị của \(F\left( { – 2} \right) + 3F\left( 4 \right)\) bằng

Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.

Ngày Thuộc chủ đề:Blog, Trắc nghiệm Sự tương giao đồ thị hàm số Tag với:,

Câu hỏi: Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình\(f\left( {f\left( x \right)} \right) = \frac{3}{2}\) là A. \(9\). B. \(6\). C. \(7\). D. \(3\). LỜI GIẢI CHI TIẾT Ta có \(f(f(x)) = \frac{3}{2} \Rightarrow \left[ \begin{array}{l}f(x) = a\quad ( - 2 < a < - 1)\quad \quad (1)\\f(x) = … [Đọc thêm...] vềCho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.