Ham so Logarit VDC

Cho \({\log _7}12 = x\), \(\,{\log _{12}}24 = y\), \({\log _{54}}168 = \frac{{a.xy + b}}{{cxy + dx}}\), với \(a,\,b,\,c,\,d\,\) là các số nguyên và \(\frac{c}{d}\) là phân số tối giản. Tính tổng \(T = \left| {a + b + c + d} \right|\) .

Ngày 19/10/2021 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:Ham so Logarit VDC

Câu hỏi: Cho \({\log _7}12 = x\), \(\,{\log _{12}}24 = y\), \({\log _{54}}168 = \frac{{a.xy + b}}{{cxy + dx}}\), với \(a,\,b,\,c,\,d\,\) là các số nguyên và \(\frac{c}{d}\) là phân số tối giản. Tính tổng \(T = \left| {a + b + c + d} \right|\) . A. \(T = 5\). B. \(T = 8\). C. \(T = 3\). D. \(T = 6\). Lời giải Ta có \({\log _7}12 = x \Leftrightarrow {\log … [Đọc thêm...] về

Cho \({\log _7}12 = x\), \(\,{\log _{12}}24 = y\), \({\log _{54}}168 = \frac{{a.xy + b}}{{cxy + dx}}\), với \(a,\,b,\,c,\,d\,\) là các số nguyên và \(\frac{c}{d}\) là phân số tối giản. Tính tổng \(T = \left| {a + b + c + d} \right|\) .

. Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f\left( x \right)\) như hình vẽ dưới đây.

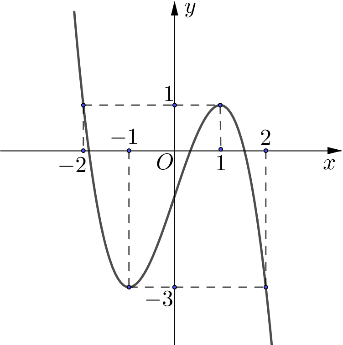
Số nghiệm thực của phương trình \(f\left( {f\left( {f\left( {{2^x}} \right)} \right)} \right) = 1\) là

Ngày 19/10/2021 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:Ham so Logarit VDC

Câu hỏi: . Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f\left( x \right)\) như hình vẽ dưới đây. Số nghiệm thực của phương trình \(f\left( {f\left( {f\left( {{2^x}} \right)} \right)} \right) = 1\) là A. \(8\). B. \(5\). C. \(3\). D. \(4\). Lời giải Theo đồ thị, ta có: \(f\left( {f\left( {f\left( {{2^x}} \right)} … [Đọc thêm...] về

. Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f\left( x \right)\) như hình vẽ dưới đây.

Số nghiệm thực của phương trình \(f\left( {f\left( {f\left( {{2^x}} \right)} \right)} \right) = 1\) là

Cho hàm số \(y = \frac{{{{3.2}^x} – 1}}{{{2^x} + m}}\) với \(m\) là tham số thực. Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) trong khoảng \(\left( { – 2020\,;\,2020} \right)\) để hàm số nghịch biến trên khoảng \(\left( {0\,;3} \right)\). Số phần tử của \(S\) là

Ngày 19/10/2021 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:Ham so Logarit VDC

Câu hỏi: Cho hàm số \(y = \frac{{{{3.2}^x} - 1}}{{{2^x} + m}}\) với \(m\) là tham số thực. Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) trong khoảng \(\left( { - 2020\,;\,2020} \right)\) để hàm số nghịch biến trên khoảng \(\left( {0\,;3} \right)\). Số phần tử của \(S\) là A. \(2011\). B. \(2012\). C. \(2013\). D. \(2014\). Lời giải Đặt … [Đọc thêm...] về

Cho hàm số \(y = \frac{{{{3.2}^x} – 1}}{{{2^x} + m}}\) với \(m\) là tham số thực. Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) trong khoảng \(\left( { – 2020\,;\,2020} \right)\) để hàm số nghịch biến trên khoảng \(\left( {0\,;3} \right)\). Số phần tử của \(S\) là

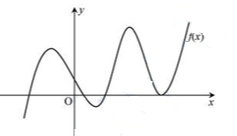
. Cho hàm số \(y = f(x)\) có đồ thị biểu diễn như hình vẽ và đồ thị đạo hàm không tiếp xúc với trục hoành. Số nghiệm của phương trình \(f(x){.2^{f'(x)}} + 2f'(x){.3^{f(x)}} = f(x) + 2f'(x)\) tương ứng là

Ngày 19/10/2021 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:Ham so Logarit VDC

Câu hỏi: . Cho hàm số \(y = f(x)\) có đồ thị biểu diễn như hình vẽ và đồ thị đạo hàm không tiếp xúc với trục hoành. Số nghiệm của phương trình \(f(x){.2^{f'(x)}} + 2f'(x){.3^{f(x)}} = f(x) + 2f'(x)\) tương ứng là A. \(6\). B. \(7\). C. \(8\). D. \(5\). Lời giải Từ đồ thị hàm số suy ra \(f(x) = 0\) có các nghiệm \({x_1} < {x_2} < {x_3} < {x_4}\) … [Đọc thêm...] về

. Cho hàm số \(y = f(x)\) có đồ thị biểu diễn như hình vẽ và đồ thị đạo hàm không tiếp xúc với trục hoành. Số nghiệm của phương trình \(f(x){.2^{f'(x)}} + 2f'(x){.3^{f(x)}} = f(x) + 2f'(x)\) tương ứng là

Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) – {{\log }_2}\left( {x + 21} \right)} \right]\left( {16 – {2^{x – 1}}} \right) \ge 0\) ?

Ngày 24/08/2021 Thuộc chủ đề:Blog, Trắc nghiệm Phương trình và bất phương trình Logarit, Trắc nghiệm Phương trình và bất phương trình mũ Tag với:Ham so Logarit VDC, HAM SO MU VDC, TN THPT 2021

Câu hỏi: Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) - {{\log }_2}\left( {x + 21} \right)} \right]\left( {16 - {2^{x - 1}}} \right) \ge 0\) ? A. Vô số. B. \[17\] . C. \[16\] . D. \[18\] . LỜI GIẢI CHI TIẾT Điều kiện: \(x > - 21\) Có \[\left[ {{{\log }_2}\left( {{x^2} + 1} \right) - {{\log }_2}\left( … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\) thỏa mãn \(\left[ {{{\log }_2}\left( {{x^2} + 1} \right) – {{\log }_2}\left( {x + 21} \right)} \right]\left( {16 – {2^{x – 1}}} \right) \ge 0\) ?

Có bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right)\) ?

Câu hỏi: Có bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x - 1} \right){e^x} = y\left( {{e^x} + xy - 2{x^2} - 3} \right)\) ? A. 17 . B. 18 . C. 16 . D. 15 . LỜI GIẢI CHI TIẾT Ta có \(4\left( {x - 1} \right){e^x} = y\left( {{e^x} + xy - 2{x^2} - 3} \right) \Leftrightarrow 4\left( {x - 1} \right){e^x} - … [Đọc thêm...] vềCó bao nhiêu số nguyên dương y sao cho tồn tại số thực \(x \in \left( {1;\,6} \right)\) thỏa mãn \(4\left( {x – 1} \right){e^x} = y\left( {{e^x} + xy – 2{x^2} – 3} \right)\) ?

Có bao nhiêu số nguyên \(x\) thỏa mãn\(\left( {{3^{{x^3}}} – \frac{1}{{{9^{x + 6}}}}} \right).\left( {{{\log }_5}\left( {x + 4} \right) – 2} \right) \le 0\). \(\left( 1 \right)\)

Ngày 05/08/2021 Thuộc chủ đề:Blog, Trắc nghiệm Phương trình và bất phương trình Logarit, Trắc nghiệm Phương trình và bất phương trình mũ Tag với:Ham so Logarit VDC, HAM SO MU VDC, TN THPT 2021

Câu hỏi: Có bao nhiêu số nguyên \(x\) thỏa mãn\(\left( {{3^{{x^3}}} - \frac{1}{{{9^{x + 6}}}}} \right).\left( {{{\log }_5}\left( {x + 4} \right) - 2} \right) \le 0\). \(\left( 1 \right)\) A. \(25\). B. \(26\). C. \(24\). D. Vô số. LỜI GIẢI CHI TIẾT Tác giả: Hương Đào Điều kiện xác định: \(x > - 4\). Với điều kiện \(x > - 4\) ta có: \(\left( … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\) thỏa mãn\(\left( {{3^{{x^3}}} – \frac{1}{{{9^{x + 6}}}}} \right).\left( {{{\log }_5}\left( {x + 4} \right) – 2} \right) \le 0\). \(\left( 1 \right)\)

Có bao nhiêu số nguyên \(x\) thỏa mãn \(\)\(\left( {\log _2^2x – 2{{\log }_2}x} \right)\left( {{3^{x + 1}} – 9} \right) \le 0\)?

Câu hỏi: Có bao nhiêu số nguyên \(x\) thỏa mãn \(\)\(\left( {\log _2^2x - 2{{\log }_2}x} \right)\left( {{3^{x + 1}} - 9} \right) \le 0\)? A. \(3\). B. \(4\). C. \(5\). D. Vô số. LỜI GIẢI CHI TIẾT Điều kiện: \(x > 0\). Cho \(\log _2^2x - 2{\log _2}x = 0 \Leftrightarrow \left[ \begin{array}{l}{\log _2}x = 0\\{\log _2}x = 2\end{array} \right. … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\) thỏa mãn \(\)\(\left( {\log _2^2x – 2{{\log }_2}x} \right)\left( {{3^{x + 1}} – 9} \right) \le 0\)?

Có bao nhiêu số nguyên \(x\)thỏa mãn \(\left( {\log _2^2x – 4{{\log }_2}x – 5} \right)\left( {{3^{{x^2} – 5x}} – 1} \right) \le 0\)?

Ngày 04/08/2021 Thuộc chủ đề:Blog, Trắc nghiệm Phương trình và bất phương trình Logarit, Trắc nghiệm Phương trình và bất phương trình mũ Tag với:Ham so Logarit VDC, HAM SO MU VDC, TN THPT 2021

Câu hỏi: Có bao nhiêu số nguyên \(x\)thỏa mãn \(\left( {\log _2^2x - 4{{\log }_2}x - 5} \right)\left( {{3^{{x^2} - 5x}} - 1} \right) \le 0\)? A. \(28\) B. \(29\) C. \(5\) D. Vô số LỜI GIẢI CHI TIẾT Điều kiện \(x > 0\left( * \right)\) -Trường hợp 1: \(\left\{ {\begin{array}{*{20}{c}}{\log _2^2x - 4{{\log }_2}x - 5 \le 0}\\{{3^{{x^2} - 5x}} - 1 \ge … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\)thỏa mãn \(\left( {\log _2^2x – 4{{\log }_2}x – 5} \right)\left( {{3^{{x^2} – 5x}} – 1} \right) \le 0\)?

Có bao nhiêu số nguyên \(x\) sao cho tồn tại \(y \in \left( {\frac{1}{{\sqrt 2 }};2} \right)\) thỏa mãn\({8^{{y^2} + xy}} = \left( {1 + 2xy} \right){.8^y}\)?

Câu hỏi: Có bao nhiêu số nguyên \(x\) sao cho tồn tại \(y \in \left( {\frac{1}{{\sqrt 2 }};2} \right)\) thỏa mãn\({8^{{y^2} + xy}} = \left( {1 + 2xy} \right){.8^y}\)? A. 3. B. 2. C. 1. D. 0. LỜI GIẢI CHI TIẾT Phương trình đã cho tương đương với \({2^{3{y^2} + 3xy - 3y}} = 1 + 2xy\). Suy ra \(1 + 2xy > 0 \Leftrightarrow x > - \frac{1}{{2y}}\), mà … [Đọc thêm...] vềCó bao nhiêu số nguyên \(x\) sao cho tồn tại \(y \in \left( {\frac{1}{{\sqrt 2 }};2} \right)\) thỏa mãn\({8^{{y^2} + xy}} = \left( {1 + 2xy} \right){.8^y}\)?