Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty+so

Người ta muốn trồng hoa trên một miếng đất hình tròn có bán kính bằng \(5\) m. Họ dự định sẽ để lại một phần (phần màu trắng như hình vẽ, trong đó \(AB = 6m\)) để làm việc khá C. Biết mỗi mét vuông trồng hoa cần chi phí 200 nghìn đồng. Hỏi cần bao nhiêu tiềnđể có thể thực hiện dự định này ?

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:,

Câu hỏi: Người ta muốn trồng hoa trên một miếng đất hình tròn có bán kính bằng \(5\) m. Họ dự định sẽ để lại một phần (phần màu trắng như hình vẽ, trong đó \(AB = 6m\)) để làm việc khá C. Biết mỗi mét vuông trồng hoa cần chi phí 200 nghìn đồng. Hỏi cần bao nhiêu tiềnđể có thể thực hiện dự định này ? A. 22335 nghìn đồng. B. \(7445\) nghìn đồng. C. 14890 nghìn đồng. … [Đọc thêm...] vềNgười ta muốn trồng hoa trên một miếng đất hình tròn có bán kính bằng \(5\) m. Họ dự định sẽ để lại một phần (phần màu trắng như hình vẽ, trong đó \(AB = 6m\)) để làm việc khá C. Biết mỗi mét vuông trồng hoa cần chi phí 200 nghìn đồng. Hỏi cần bao nhiêu tiềnđể có thể thực hiện dự định này ?

Người ta phân khu vườn hình chữ nhật \(ABCD\), \(AB = 10{\rm{m}}\), \(AD = 20{\rm{m}}\)thành năm khu vực bởi bốn parabol rồi trồng hoa ở khu vực trung tâm như hình vẽ kèm theo. Trong đó:➀ Hai parabol kề nhau tiếp xúc nhau tại một trong các điểm \(A,\,B,\,C,\,D\).➁ Khu vực trồng hoa là một hình có hai trục đối xứng.Với việc làm như đã nêu thì diện tích của khu vực trồng hoa có thể đạt giá trị lớn nhất là bao nhiêu?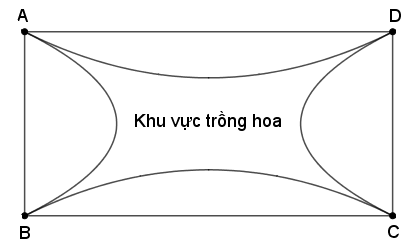

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:,

Câu hỏi: Người ta phân khu vườn hình chữ nhật \(ABCD\), \(AB = 10{\rm{m}}\), \(AD = 20{\rm{m}}\)thành năm khu vực bởi bốn parabol rồi trồng hoa ở khu vực trung tâm như hình vẽ kèm theo. Trong đó:➀ Hai parabol kề nhau tiếp xúc nhau tại một trong các điểm \(A,\,B,\,C,\,D\).➁ Khu vực trồng hoa là một hình có hai trục đối xứng.Với việc làm như đã nêu thì diện tích của khu vực … [Đọc thêm...] vềNgười ta phân khu vườn hình chữ nhật \(ABCD\), \(AB = 10{\rm{m}}\), \(AD = 20{\rm{m}}\)thành năm khu vực bởi bốn parabol rồi trồng hoa ở khu vực trung tâm như hình vẽ kèm theo. Trong đó:➀ Hai parabol kề nhau tiếp xúc nhau tại một trong các điểm \(A,\,B,\,C,\,D\).➁ Khu vực trồng hoa là một hình có hai trục đối xứng.Với việc làm như đã nêu thì diện tích của khu vực trồng hoa có thể đạt giá trị lớn nhất là bao nhiêu?

Cho hình nón chứa năm mặt cầu cùng có bán kính là 1, trong đó bốn mặt cầu tiếp xúc với đáy, tiếp xúc đôi một với nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ năm tiếp xúc với bốn mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy hình nón.

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Cho hình nón chứa năm mặt cầu cùng có bán kính là 1, trong đó bốn mặt cầu tiếp xúc với đáy, tiếp xúc đôi một với nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ năm tiếp xúc với bốn mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy hình nón. A. \(2\sqrt 3 + 1\). B. \(2\sqrt 2 + 1\). C. \(2\sqrt 2 - 1\). D. \(3\sqrt 2 + … [Đọc thêm...] vềCho hình nón chứa năm mặt cầu cùng có bán kính là 1, trong đó bốn mặt cầu tiếp xúc với đáy, tiếp xúc đôi một với nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ năm tiếp xúc với bốn mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy hình nón.

Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng \(9\,{\rm{cm}}\). Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.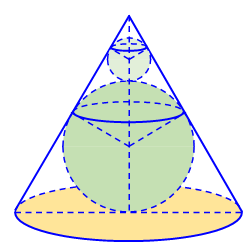

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của … [Đọc thêm...] vềNgười ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng \(9\,{\rm{cm}}\). Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.

(Chuyên Vinh – 2022) Trong không gian \(Oxyz\), cho mặt phẳng \((P):2x – y + 2z + 16 = 0\) và mặt cầu \((S):{(x – 2)^2} + {(y + 1)^2} + {(z – 3)^2} = 21\). Một khối hộp chữ nhật \((H)\) có bốn đỉnh nằm trên mặt phẳng \((P)\) và bốn đỉnh còn lại nằm trên mặt cầu \((S)\). Khi \((H)\) có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của \((H)\) nằm trên mặt cầu \((S)\) là \((Q):2x + by + cz + d = 0\). Giá trị \(b + c + d\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:,

Câu hỏi: (Chuyên Vinh – 2022) Trong không gian \(Oxyz\), cho mặt phẳng \((P):2x - y + 2z + 16 = 0\) và mặt cầu \((S):{(x - 2)^2} + {(y + 1)^2} + {(z - 3)^2} = 21\). Một khối hộp chữ nhật \((H)\) có bốn đỉnh nằm trên mặt phẳng \((P)\) và bốn đỉnh còn lại nằm trên mặt cầu \((S)\). Khi \((H)\) có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của \((H)\) nằm trên mặt cầu … [Đọc thêm...] về

(Chuyên Vinh – 2022) Trong không gian \(Oxyz\), cho mặt phẳng \((P):2x – y + 2z + 16 = 0\) và mặt cầu \((S):{(x – 2)^2} + {(y + 1)^2} + {(z – 3)^2} = 21\). Một khối hộp chữ nhật \((H)\) có bốn đỉnh nằm trên mặt phẳng \((P)\) và bốn đỉnh còn lại nằm trên mặt cầu \((S)\). Khi \((H)\) có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của \((H)\) nằm trên mặt cầu \((S)\) là \((Q):2x + by + cz + d = 0\). Giá trị \(b + c + d\) bằng

(Cụm Trường Nghệ An – 2022) Cắt hình nón \(\left( N \right)\) bởi mặt phẳng đi qua đỉnh \(S\) và tạo với trục của \(\left( N \right)\) một góc bằng \(30^\circ \), ta được thiết diện là tam giác \(SAB\) vuông và có diện tích bằng \(4{a^2}\).Chiều cao của hình nón bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (Cụm Trường Nghệ An - 2022) Cắt hình nón \(\left( N \right)\) bởi mặt phẳng đi qua đỉnh \(S\) và tạo với trục của \(\left( N \right)\) một góc bằng \(30^\circ \), ta được thiết diện là tam giác \(SAB\) vuông và có diện tích bằng \(4{a^2}\).Chiều cao của hình nón bằng A. \(a\sqrt 3 \). B. \(2a\sqrt 3 \). C. \(2a\sqrt 2 \). D. \(a\sqrt 2 \). Lời … [Đọc thêm...] về

(Cụm Trường Nghệ An – 2022) Cắt hình nón \(\left( N \right)\) bởi mặt phẳng đi qua đỉnh \(S\) và tạo với trục của \(\left( N \right)\) một góc bằng \(30^\circ \), ta được thiết diện là tam giác \(SAB\) vuông và có diện tích bằng \(4{a^2}\).Chiều cao của hình nón bằng

(Chuyên Hạ Long 2022) Cho hình chóp \(S \cdot ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA = a\sqrt 7 \) và vuông góc với đáy. Lấy điểm \(M\) trên cạnh \(SC\) sao cho \(CM < a\). Gọi \((C)\) là hình nón có đỉnh \(C\), các điểm \(B,M,D\) thuộc mặt xung quanh, điểm \(A\) thuộc mặt đáy của hình nón. Tính diện tích xung quanh của \((C)\).

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (Chuyên Hạ Long 2022) Cho hình chóp \(S \cdot ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA = a\sqrt 7 \) và vuông góc với đáy. Lấy điểm \(M\) trên cạnh \(SC\) sao cho \(CM < a\). Gọi \((C)\) là hình nón có đỉnh \(C\), các điểm \(B,M,D\) thuộc mặt xung quanh, điểm \(A\) thuộc mặt đáy của hình nón. Tính diện tích xung quanh của \((C)\). A. … [Đọc thêm...] về

(Chuyên Hạ Long 2022) Cho hình chóp \(S \cdot ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA = a\sqrt 7 \) và vuông góc với đáy. Lấy điểm \(M\) trên cạnh \(SC\) sao cho \(CM < a\). Gọi \((C)\) là hình nón có đỉnh \(C\), các điểm \(B,M,D\) thuộc mặt xung quanh, điểm \(A\) thuộc mặt đáy của hình nón. Tính diện tích xung quanh của \((C)\).

(THPT Nguyễn Tất Thành-Đh-SP-HN-2022) Cho \(x,y,z \in \left[ {0;2} \right]\) và thỏa mãn \(x + 2y + z = 6\). Tìm giá trị lớn nhất của biểu thức \(P = {3^{2x – {x^2}}} + {5^{2y – {y^2}}} + {3^z} + 2{x^2} + 4{y^2}\)

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:, ,

Câu hỏi: (THPT Nguyễn Tất Thành-Đh-SP-HN-2022) Cho \(x,y,z \in \left[ {0;2} \right]\) và thỏa mãn \(x + 2y + z = 6\). Tìm giá trị lớn nhất của biểu thức \(P = {3^{2x - {x^2}}} + {5^{2y - {y^2}}} + {3^z} + 2{x^2} + 4{y^2}\) A. \(\max P = 25\). B.\(\max P = 27\). C.\(\max P = 26\). D.\(\max P = 30\). Lời giải: Chọn B Xét hàm số \(f\left( t \right) = … [Đọc thêm...] về

(THPT Nguyễn Tất Thành-Đh-SP-HN-2022) Cho \(x,y,z \in \left[ {0;2} \right]\) và thỏa mãn \(x + 2y + z = 6\). Tìm giá trị lớn nhất của biểu thức \(P = {3^{2x – {x^2}}} + {5^{2y – {y^2}}} + {3^z} + 2{x^2} + 4{y^2}\)

Giải bài Ôn tập hình học và đo lường | Giải toán 3 tập 2 chân trời sáng tạo

Ngày Thuộc chủ đề:Giải bài tập Toán 3 - Chân trời Tag với:

Giải bài tập thực hành Giải bài Ôn tập hình học và đo lường | Giải toán 3 tập 2 chân trời sáng tạo ============ Chuyên mục: Giải bài tập Toán 3 - Chân trời ============= LUYỆN TẬP Bài tập 1. Trang 82 sgk toán 3 tập 2 Số?a) 1 m = .?.  dm                                 1 km =  .?.  m           =  .?.  cm                                1 dm =  .?.  cm           =  .?.  … [Đọc thêm...] vềGiải bài Ôn tập hình học và đo lường | Giải toán 3 tập 2 chân trời sáng tạo

Giải bài Ôn tập các phép tính | Giải toán 3 tập 2 chân trời sáng tạo

Ngày Thuộc chủ đề:Giải bài tập Toán 3 - Chân trời Tag với:

Giải bài tập thực hành Giải bài Ôn tập các phép tính | Giải toán 3 tập 2 chân trời sáng tạo ============ Chuyên mục: Giải bài tập Toán 3 - Chân trời ============= LUYỆN TẬP Bài tập 1. Trang 80 sgk toán 3 tập 2 Đặt tính rồi tính.a) 37 652 + 4 239                                        b) 77 208 – 68 196c) 10 813 x 6                                                d) 8 438 … [Đọc thêm...] vềGiải bài Ôn tập các phép tính | Giải toán 3 tập 2 chân trời sáng tạo