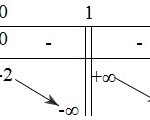
Đề bài: Chứng minh rằng nếu hàm số \(f(x)\) xác định và liên tục trên \([a;b]\) thì với các điểm \(x_{1},x_{2},...,x_{n}\) bất kì thuộc \([a;b]\) đều có một số \(c\in [a;b]\) sao cho \(f(c)=\frac{1}{n}[f(x_{1})+f(x_{2})+...+f(x_{n})]\). Lời giải Nếu \(x_{1},x_{2},...,x_{n}\)thuộc \([a;b]\) ta có \(f(x_{1})=f(x_{2})=...=f(x_{n})\) thì rõ ràng lấy \(c=x_{1}\in … [Đọc thêm...] vềĐề: Chứng minh rằng nếu hàm số \(f(x)\) xác định và liên tục trên \([a;b]\) thì với các điểm \(x_{1},x_{2},…,x_{n}\) bất kì thuộc \([a;b]\) đều có một số \(c\in [a;b]\) sao cho \(f(c)=\frac{1}{n}[f(x_{1})+f(x_{2})+…+f(x_{n})]\).
Bài tập Hàm số
Đề: Trên mặt phẳng tọa độ cho điểm $A(3 , 0)$ và parabol $(P)$ có phương trình $y = {x^2}$.a) $M$ là một điểm thuộc parabol $(P)$, có hoành độ ${x_M} = a$. Tính độ dài đoạn $AM$, xác định $a$ để $AM$ ngắn nhất.b) Chứng tỏ rằng nếu đoạn $AM$ ngắn nhất, thì $AM$ vuông góc với tiếp tuyến tại $M$ của parabol $(P)$
Đề bài: Trên mặt phẳng tọa độ cho điểm $A(3 , 0)$ và parabol $(P)$ có phương trình $y = {x^2}$.a) $M$ là một điểm thuộc parabol $(P)$, có hoành độ ${x_M} = a$. Tính độ dài đoạn $AM$, xác định $a$ để $AM$ ngắn nhất.b) Chứng tỏ rằng nếu đoạn $AM$ ngắn nhất, thì $AM$ vuông góc với tiếp tuyến tại $M$ của parabol $(P)$ Lời giải a) ${x_M} = a \Rightarrow {y_M} = {a^2}$. Do … [Đọc thêm...] vềĐề: Trên mặt phẳng tọa độ cho điểm $A(3 , 0)$ và parabol $(P)$ có phương trình $y = {x^2}$.a) $M$ là một điểm thuộc parabol $(P)$, có hoành độ ${x_M} = a$. Tính độ dài đoạn $AM$, xác định $a$ để $AM$ ngắn nhất.b) Chứng tỏ rằng nếu đoạn $AM$ ngắn nhất, thì $AM$ vuông góc với tiếp tuyến tại $M$ của parabol $(P)$
Đề: Tìm hai điểm $A,B$ nằm trên đồ thị $(C):y=\frac{x^2}{x-1}$ và đối xứng nhau qua đường thẳng $(d):y=x-1$
Đề bài: Tìm hai điểm $A,B$ nằm trên đồ thị $(C):y=\frac{x^2}{x-1}$ và đối xứng nhau qua đường thẳng $(d):y=x-1$ Lời giải Hai điểm $A,B$ đối xứng nhau qua đường thẳng $(d)$.$\Leftrightarrow AB\bot (d)$ và trung điểm $I$ của $AB$ thuộc $(d)$.*Vì $AB$ vuông góc với $(d)$ nên $(AB):y=-x+m$.Hoành độ giao điểm $A,B$ là nghiệm của phương trình:$\frac{x^{2}}{x-1}=-x+m … [Đọc thêm...] vềĐề: Tìm hai điểm $A,B$ nằm trên đồ thị $(C):y=\frac{x^2}{x-1}$ và đối xứng nhau qua đường thẳng $(d):y=x-1$
Đề: $1$. Khảo sát hàm số \(y = \frac{{{x^2} + x – 5}}{{x – 2}}\left( C \right)\)$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất
Đề bài: $1$. Khảo sát hàm số \(y = \frac{{{x^2} + x - 5}}{{x - 2}}\left( C \right)\)$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất Lời giải $1$. Bạn đọc tự giải.$2$. Đồ thị có tiệm cận đứng \(x … [Đọc thêm...] vềĐề: $1$. Khảo sát hàm số \(y = \frac{{{x^2} + x – 5}}{{x – 2}}\left( C \right)\)$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất
Đề: Cho hàm số $y=-\frac{1}{3}x^2-2x^2+3x $ có đồ thị $(C)$. Viết phương trình tiếp tuyến $\Delta $ của $(C)$ tại điểm uốn và chứng minh rằng $\Delta $ là tiếp tuyến cho hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của $(C)$
Đề bài: Cho hàm số $y=-\frac{1}{3}x^2-2x^2+3x $ có đồ thị $(C)$. Viết phương trình tiếp tuyến $\Delta $ của $(C)$ tại điểm uốn và chứng minh rằng $\Delta $ là tiếp tuyến cho hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của $(C)$ Lời giải Dễ thấy điểm uốn của đồ thị là $U\left ( 2;\frac{2}{3} \right )$. Tại $U$ tiếp tuyến của $(C)$ có hệ số góc $y'(2)=-1$. Tiếp tuyến … [Đọc thêm...] vềĐề: Cho hàm số $y=-\frac{1}{3}x^2-2x^2+3x $ có đồ thị $(C)$. Viết phương trình tiếp tuyến $\Delta $ của $(C)$ tại điểm uốn và chứng minh rằng $\Delta $ là tiếp tuyến cho hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của $(C)$
Đề: Định $m$ để hàm số :$y=\sqrt{mx-2m+1}+\sqrt{2x+m-2} $ xác định khi $x \geq 1$
Đề bài: Định $m$ để hàm số :$y=\sqrt{mx-2m+1}+\sqrt{2x+m-2} $ xác định khi $x \geq 1$ Lời giải ĐS: $0 \leq m \leq 1$thêm lời giải chi tiết … [Đọc thêm...] vềĐề: Định $m$ để hàm số :$y=\sqrt{mx-2m+1}+\sqrt{2x+m-2} $ xác định khi $x \geq 1$
Đề: Khảo sát sự biến thiên của hàm số $y=x^2+2x-2$ trên mỗi khoảng $(-\infty ;-1)$ và $(-1;+\infty .)$
Đề bài: Khảo sát sự biến thiên của hàm số $y=x^2+2x-2$ trên mỗi khoảng $(-\infty ;-1)$ và $(-1;+\infty .)$ Lời giải Xét tỷ số : $\frac{f(x_{2})-f(x_{1} ) }{x_{2} -x_{1} } =\frac{(x_{2}^2+2 x_{2}-2)-(x_{1}^2+2 x_{1}-2)}{x_{2}- x_{1} } = x_{1}+x_{2}+2.$ Trên khoảng $(-\infty ;-1)$ ta có $x_{1}nên suy ra hàm số nghịch biến.Tương tự, trên khoảng $(-1;+\infty )$, ta có … [Đọc thêm...] vềĐề: Khảo sát sự biến thiên của hàm số $y=x^2+2x-2$ trên mỗi khoảng $(-\infty ;-1)$ và $(-1;+\infty .)$
Đề: Cho hàm số $y=\frac{x^2+x-1}{x+1} $ có đồ thị $(C)$. Chứng minh rằng trên $(C)$ luôn có hai điểm mà tiếp tuyến tại đó song song với nhau.
Đề bài: Cho hàm số $y=\frac{x^2+x-1}{x+1} $ có đồ thị $(C)$. Chứng minh rằng trên $(C)$ luôn có hai điểm mà tiếp tuyến tại đó song song với nhau. Lời giải Cần giải chi tiết:Giả sử $x_1\neq x_2$. Ta chứng minh rằng $y'(x_1)=y'(x_2)$ … [Đọc thêm...] vềĐề: Cho hàm số $y=\frac{x^2+x-1}{x+1} $ có đồ thị $(C)$. Chứng minh rằng trên $(C)$ luôn có hai điểm mà tiếp tuyến tại đó song song với nhau.
Đề: $1.$Khảo sát sự biến thiên và vẽ đồ thị hàm số:$y = \frac{x^2 – 2x + 2}{x – 1}$$2.$ Tìm giá trị lớn nhất và giá trị bé nhất của hàm số:$y = {\mathop{ sinx}} – cos^2x + \frac{1}{2}$
Đề bài: $1.$Khảo sát sự biến thiên và vẽ đồ thị hàm số:$y = \frac{x^2 - 2x + 2}{x - 1}$$2.$ Tìm giá trị lớn nhất và giá trị bé nhất của hàm số:$y = {\mathop{ sinx}} - cos^2x + \frac{1}{2}$ Lời giải $1.$ * TXĐ: $R\setminus \left\{ {1} \right\} $* Sự biến thiên:$\mathop {\lim }\limits_{x \to +\infty } \frac{x^2-2x+2}{x-1} =\frac{x-2+\frac{2}{x} }{1-\frac{1}{x} }=+ \infty … [Đọc thêm...] vềĐề: $1.$Khảo sát sự biến thiên và vẽ đồ thị hàm số:$y = \frac{x^2 – 2x + 2}{x – 1}$$2.$ Tìm giá trị lớn nhất và giá trị bé nhất của hàm số:$y = {\mathop{ sinx}} – cos^2x + \frac{1}{2}$
Đề: Xét tính chẵn, lẻ của các hàm số :$a) f(x) = x + tanx + sinx$ $b$) $f(x) = \frac{{\left| {x – 1} \right|cosx}}{{\sqrt {{{\left( {x – 1} \right)}^2}} }}$$c)$ $f(x) = \frac{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} – x + 1} }}{{{x^2}}}$
Đề bài: Xét tính chẵn, lẻ của các hàm số :$a) f(x) = x + tanx + sinx$ $b$) $f(x) = \frac{{\left| {x - 1} \right|cosx}}{{\sqrt {{{\left( {x - 1} \right)}^2}} }}$$c)$ $f(x) = \frac{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} - x + 1} }}{{{x^2}}}$ Lời giải $a) f(x) = x + tgx + sinx $Miền xác định : $D=R\left\{ \begin{array}{l} x/x=\frac{\pi}{2}+k\pi,k\in … [Đọc thêm...] vềĐề: Xét tính chẵn, lẻ của các hàm số :$a) f(x) = x + tanx + sinx$ $b$) $f(x) = \frac{{\left| {x – 1} \right|cosx}}{{\sqrt {{{\left( {x – 1} \right)}^2}} }}$$c)$ $f(x) = \frac{{\sqrt {{x^2} + x + 1} + \sqrt {{x^2} – x + 1} }}{{{x^2}}}$