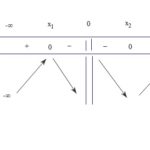
Đề bài: Tính đạo hàm cấp $n$ của hàm số \(y = \sin^2x\), từ đó suy ra đọa hàm cấp $n$ của hàm số \(y = \cos^2x\) Lời giải Ta có:\(\begin{array}{l}\left( {\sin x} \right)' = \cos x = \sin \left( {x + \frac{\pi }{2}} \right)\\\left( {\cos x} \right)' =- {\mathop{\rm s}\nolimits} {\rm{inx}} = c{\rm{os}}\left( {x + \frac{\pi }{2}} \right)\end{array}\)Do đó: \(\begin{array}{l}y … [Đọc thêm...] vềĐề: Tính đạo hàm cấp $n$ của hàm số \(y = \sin^2x\), từ đó suy ra đọa hàm cấp $n$ của hàm số \(y = \cos^2x\)
Bài tập Hàm số
Đề: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$ $b)$ Qua điểm $A(1, 0)$ viết phương trình tiếp tuyến với đồ thị
Đề bài: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} - 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$ $b)$ Qua điểm $A(1, 0)$ viết phương trình tiếp tuyến với đồ thị Lời giải $1$. Ta có:\(\begin{array}{l}y = \frac{{{x^2} + {m^2}x + 2{m^2} - 5m + 3}}{x} … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$ $b)$ Qua điểm $A(1, 0)$ viết phương trình tiếp tuyến với đồ thị
Đề: Xác định $m$ để các hàm số sau đấy xác định với mọi $x>0$a) $y=\sqrt{x-m}+\sqrt{2x-m-1}$ b) $y=\sqrt{2x-3m+4}+\frac{x-m}{x+m-1}$
Đề bài: Xác định $m$ để các hàm số sau đấy xác định với mọi $x>0$a) $y=\sqrt{x-m}+\sqrt{2x-m-1}$ b) $y=\sqrt{2x-3m+4}+\frac{x-m}{x+m-1}$ Lời giải Giảia) Hàm số $y$ xác định $\Leftrightarrow \begin{cases}x-m \geq 0 \\ 2x-m-1 \geq 0 \end{cases} \Leftrightarrow \begin{cases}x \geq m (1) \\ x \geq \frac{m+1}{2} (2) \end{cases}$Do đó … [Đọc thêm...] vềĐề: Xác định $m$ để các hàm số sau đấy xác định với mọi $x>0$a) $y=\sqrt{x-m}+\sqrt{2x-m-1}$ b) $y=\sqrt{2x-3m+4}+\frac{x-m}{x+m-1}$
Đề: a) Tìm tập giá trị của các hàm số $y=x^{2}$b) Với giá trị nào của $x$ thì hàm số $y=0$$y=2x-6; y=x^{2}-25$
Đề bài: a) Tìm tập giá trị của các hàm số $y=x^{2}$b) Với giá trị nào của $x$ thì hàm số $y=0$$y=2x-6; y=x^{2}-25$ Lời giải a) Hàm số $y=x^{2}$ xác định với mọi giá trị của $x$ ( nghĩa là $D=R$) và tập giá trị của hàm số là $[0;+\infty)$b) $y=2x-6, y=0$ thì $2x-6=0\Leftrightarrow x=3$$y=x^{2}-25, y=0$ thì $x^{2}-25=0\Leftrightarrow x=\pm5$ … [Đọc thêm...] vềĐề: a) Tìm tập giá trị của các hàm số $y=x^{2}$b) Với giá trị nào của $x$ thì hàm số $y=0$$y=2x-6; y=x^{2}-25$
Đề: Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của: $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$
Đề bài: Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của: $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$ Lời giải Giải:Theo giả thiết: $\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=1$Ta có: $P=\frac{(x-1)+(y-1)}{x^2}+\frac{(y-1)+(z-1)}{y^2}+\frac{(z-1)+(x-z)}{z^2}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$ … [Đọc thêm...] vềĐề: Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của: $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$
Đề: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 – \left| x \right|}}$$ a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$ b)$ Tìm $g_0f$ và $f_0g.$
Đề bài: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 - \left| x \right|}}$$ a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$ b)$ Tìm $g_0f$ và $f_0g.$ Lời giải $a)$ $f(x) = \frac{x}{{1 + \left| x \right|}}$ có miền xác định : $D = R$ $f( - x) = - \frac{x}{{1 + \left| x \right|}} = -f(x) \Rightarrow … [Đọc thêm...] vềĐề: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 – \left| x \right|}}$$ a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$ b)$ Tìm $g_0f$ và $f_0g.$
Đề: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2} nếu x\leq -\frac{1}{2} \\ -2x^2+x+3, nếu x>-\frac{1}{2} \end{cases}$
Đề bài: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2} nếu x\leq -\frac{1}{2} \\ -2x^2+x+3, nếu x>-\frac{1}{2} \end{cases}$ Lời giải Giải* Xét hàm số bậc nhất $f_1(X)=-x+\frac{3}{2}$ trên khoảng $D_1=(-\infty; -\frac{1}{2}]$Đó là hàm số bậc nhất có $a=-1Tại $x=-\frac{1}{2}, f(-\frac{1}{2})=2$. Tại $x=\frac{3}{2}, f(\frac{3}{2})=0$Đồ thị là đường … [Đọc thêm...] vềĐề: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2} nếu x\leq -\frac{1}{2} \\ -2x^2+x+3, nếu x>-\frac{1}{2} \end{cases}$
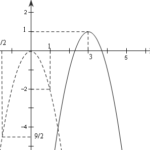
Đề: Vẽ đồ thị của hàm số $y=-2x^2+12x-17.$
Đề bài: Vẽ đồ thị của hàm số $y=-2x^2+12x-17.$ Lời giải Ta biến đổi:$y=-2x^2+12x-17=-2(x-3)^2+1.$Từ đó, đồ thị của hàm số $y=-2x^2+12x-17$ được suy từ đồ thị của hàm số $y=-2x^2$ như hình vẽ.Bây giờ sau khi biết rằng đồ thị $(P)$ của hàm số $y=ax^2+bx+c$ là một parabol như trên, để vẽ nó ta thực hiện như sau:- Xác định đỉnh của $(P)$.- Xác định trục đối xứng và hướng bề … [Đọc thêm...] vềĐề: Vẽ đồ thị của hàm số $y=-2x^2+12x-17.$
Đề: Cho hàm số : $y= – x^{4}- x^{2}+6$a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$
Đề bài: Cho hàm số : $y= - x^{4}- x^{2}+6$a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$ Lời giải a) • Tập xác định : $D=R$• Sự biến thiên : $y’=-4x^{3}-2x=-2x \left( 2 x^{2} +1 \right) =0$$\Leftrightarrow x=0 \Rightarrow y=6$Bảng … [Đọc thêm...] vềĐề: Cho hàm số : $y= – x^{4}- x^{2}+6$a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$
Đề: a) Cho hàm số phân thức dạng $ y=\frac{u}{v}; u, v $ là hàm số của $x$ và có đạo hàm, $v(x)\neq 0$. Chứng minh rằng nếu $y'(x_0)=0$ thì $y(x_0)=\frac{u'(x_0)}{v'(x_0)} $ . b) Cho hàm số $y=\frac{x^2+x-1}{x-1} $. Xác định tọa độ các điểm mà tiếp tuyến tại đó song song với trục hoành.
Đề bài: a) Cho hàm số phân thức dạng $ y=\frac{u}{v}; u, v $ là hàm số của $x$ và có đạo hàm, $v(x)\neq 0$. Chứng minh rằng nếu $y'(x_0)=0$ thì $y(x_0)=\frac{u'(x_0)}{v'(x_0)} $ . b) Cho hàm số $y=\frac{x^2+x-1}{x-1} $. Xác định tọa độ các điểm mà tiếp tuyến tại đó song song với trục hoành. Lời giải a) $\frac{u}{v} \Rightarrow … [Đọc thêm...] vềĐề: a) Cho hàm số phân thức dạng $ y=\frac{u}{v}; u, v $ là hàm số của $x$ và có đạo hàm, $v(x)\neq 0$. Chứng minh rằng nếu $y'(x_0)=0$ thì $y(x_0)=\frac{u'(x_0)}{v'(x_0)} $ . b) Cho hàm số $y=\frac{x^2+x-1}{x-1} $. Xác định tọa độ các điểm mà tiếp tuyến tại đó song song với trục hoành.