Đề bài: Cho hàm số: $y = \frac{3(x + 1)}{x - 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên. Lời giải $1.$ Bạn đọc tự giải$2.$ Phương trình tiếp tuyến tại điểm $M_0(x_0,y_0)\in (C)$ là$y=-\frac{9}{(x_0-2)^2}(x-x_0)+y_0 … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{3(x + 1)}{x – 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên.
Bài tập Hàm số
Đề: Cho hàm số $y = {(x + 1)^2}(2 – x)$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Dựa vào đồ thị, biện luận theo $m$ số nghiệm của phương trình ${(x + 1)^2}(2 – x) = {(m + 1)^2}(2 – m)$
Đề bài: Cho hàm số $y = {(x + 1)^2}(2 - x)$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Dựa vào đồ thị, biện luận theo $m$ số nghiệm của phương trình ${(x + 1)^2}(2 - x) = {(m + 1)^2}(2 - m)$ Lời giải $1)$ Hàm số xác định với mọi x.Ta có$y' = 2(x + 1)(2 - x) - {(x + 1)^2} = 3(x + 1)(1 - x)$;$y'' = 3(1 - x) - 3(1 + x) = - 6x$Bạn đọc vẽ bảng biến thiên và đồ thị … [Đọc thêm...] vềĐề: Cho hàm số $y = {(x + 1)^2}(2 – x)$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Dựa vào đồ thị, biện luận theo $m$ số nghiệm của phương trình ${(x + 1)^2}(2 – x) = {(m + 1)^2}(2 – m)$
Đề: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$. b) $Q(x;y)=(x+1)(4y+3)$
Đề bài: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$. b) $Q(x;y)=(x+1)(4y+3)$ Lời giải a) $P(x;y)=x^2+y^2=(x+y)^2-2xy=(x+y)^2-8$Theo hệ quả của bất đẳng thức Côsi cho x và y dương:$(x+y)^2\geq 4xy=16$. Tích $xy=4$ là hằng số nên tổng $x+y$ nhỏ nhất khi $x=y=2$.Vậy: min $P(x;y)=4^2-8=8$ đạt được khi … [Đọc thêm...] vềĐề: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$. b) $Q(x;y)=(x+1)(4y+3)$
Đề: Cho $y=\sqrt{\cos ^2 x -2 \cos x +5} + \sqrt{\cos ^2 x – 4 \cos x +8.} $ Tìm $max y , min y.$
Đề bài: Cho $y=\sqrt{\cos ^2 x -2 \cos x +5} + \sqrt{\cos ^2 x - 4 \cos x +8.} $ Tìm $max y , min y.$ Lời giải $y=\sqrt{(1-\cos x)^2+2^2}+\sqrt{(2-\cos x)^2+2^2}\\\le\sqrt{(1+1)^2+2^2}+\sqrt{(2+1)^2+2^2}=2\sqrt2+\sqrt{13}$$y=\sqrt{(1-\cos x)^2+2^2}+\sqrt{(2-\cos x)^2+2^2}\\\ge\sqrt{(1-1)^2+2^2}+\sqrt{(2-1)^2+2^2}=2+\sqrt5$Vậy $\max y =2\sqrt2 + \sqrt{13} $ khi … [Đọc thêm...] vềĐề: Cho $y=\sqrt{\cos ^2 x -2 \cos x +5} + \sqrt{\cos ^2 x – 4 \cos x +8.} $ Tìm $max y , min y.$
Đề: Cho phương trình bậc hai : ${x^2} – ( {2\sin \alpha – 1} )x + 6{\sin ^2}\alpha – \sin \alpha – 1 = 0$Trong đó $\alpha $ là tham sốa) Với những giá trị nào của $\alpha $ thì phương trình có nghiệm ?b) Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức ${x^2}_1 + {x^2}_2$ khi $\alpha $ thay đổi.
Đề bài: Cho phương trình bậc hai : ${x^2} - ( {2\sin \alpha - 1} )x + 6{\sin ^2}\alpha - \sin \alpha - 1 = 0$Trong đó $\alpha $ là tham sốa) Với những giá trị nào của $\alpha $ thì phương trình có nghiệm ?b) Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức ${x^2}_1 + {x^2}_2$ khi $\alpha $ thay đổi. Lời giải a) … [Đọc thêm...] vềĐề: Cho phương trình bậc hai : ${x^2} – ( {2\sin \alpha – 1} )x + 6{\sin ^2}\alpha – \sin \alpha – 1 = 0$Trong đó $\alpha $ là tham sốa) Với những giá trị nào của $\alpha $ thì phương trình có nghiệm ?b) Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức ${x^2}_1 + {x^2}_2$ khi $\alpha $ thay đổi.
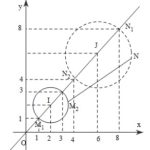
Đề: Cho $a,b,c,d$ là bốn số thực thỏa mãn các điều kiện: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases}$ Tìm GTLN, GTNN của biểu thức: $S=(a-c)^2+(b-d)^2$
Đề bài: Cho $a,b,c,d$ là bốn số thực thỏa mãn các điều kiện: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases}$ Tìm GTLN, GTNN của biểu thức: $S=(a-c)^2+(b-d)^2$ Lời giải Ta có: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases} \Leftrightarrow \begin{cases}(a-2)^2+(b-2)^2=2 \\ (c-6)^2+(d-6)^2=8 \end{cases}$ (I)Trong mặt phẳng tọa … [Đọc thêm...] vềĐề: Cho $a,b,c,d$ là bốn số thực thỏa mãn các điều kiện: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases}$ Tìm GTLN, GTNN của biểu thức: $S=(a-c)^2+(b-d)^2$
Đề: a) Vẽ đồ thị $(P)$ của hàm số $y=2x^2$.b) Trên đồ thị $(P)$ ta lấy hai điểm $A, B$ có hoành độ tương ứng là $1$ và $2$. Xác định các giá trị của $m$ và $n$ để đường thẳng $y=mx+n$ tiếp xúc với $(P)$ và song song $AB$.
Đề bài: a) Vẽ đồ thị $(P)$ của hàm số $y=2x^2$.b) Trên đồ thị $(P)$ ta lấy hai điểm $A, B$ có hoành độ tương ứng là $1$ và $2$. Xác định các giá trị của $m$ và $n$ để đường thẳng $y=mx+n$ tiếp xúc với $(P)$ và song song $AB$. Lời giải a) Học sinh tự vẽ hìnhb) Viết phương trình đường thẳng qua $A(1; 2)$ và $B(2;8)$.có dạng $\frac{x-1}{2-1}=\frac{y-2}{8-2}\Leftrightarrow … [Đọc thêm...] vềĐề: a) Vẽ đồ thị $(P)$ của hàm số $y=2x^2$.b) Trên đồ thị $(P)$ ta lấy hai điểm $A, B$ có hoành độ tương ứng là $1$ và $2$. Xác định các giá trị của $m$ và $n$ để đường thẳng $y=mx+n$ tiếp xúc với $(P)$ và song song $AB$.
Đề: Chứng minh rằng với $\forall x>0$ luôn có $\ln (x+1)
Đề bài: Chứng minh rằng với $\forall x>0$ luôn có $\ln (x+1) Lời giải Chúng ta viết lại bất đẳng thức để làm xuất hiện hàm $F$ : $ \displaystyle \ln (x+1)-00$ nên phép chia không làm đổi dấu)Xét hàm số $F(t)=\ln t$ khả vi và liên tục trên $[1,x+1]$ với $x>0$ theo định lí Lagrange luôn tồn tại $c\in(1,x+1)$ sao cho: … [Đọc thêm...] vềĐề: Chứng minh rằng với $\forall x>0$ luôn có $\ln (x+1)
Đề: Cho hàm số \(y=f(x)\) có đạo hàm với mọi \(x\) thuộc miền xác định. Chứng minh:a) Nếu \(f(x)\) là hàm số chẵn thì \(f'(x)\) là hàm số lẻ.b) Nếu \(f(x)\) là hàm số lẻ thì \(f'(x)\) là hàm số chẵn.
Đề bài: Cho hàm số \(y=f(x)\) có đạo hàm với mọi \(x\) thuộc miền xác định. Chứng minh:a) Nếu \(f(x)\) là hàm số chẵn thì \(f'(x)\) là hàm số lẻ.b) Nếu \(f(x)\) là hàm số lẻ thì \(f'(x)\) là hàm số chẵn. Lời giải a) Ta có: \(f'(-x)=\mathop {\lim }\limits_{\Delta x \to 0}\frac{f(-x+\Delta x)-f(-x)}{\Delta x}\)(1)Vì \(f(x)\) là hàm số chẵn nên \(f(-x+\Delta … [Đọc thêm...] vềĐề: Cho hàm số \(y=f(x)\) có đạo hàm với mọi \(x\) thuộc miền xác định. Chứng minh:a) Nếu \(f(x)\) là hàm số chẵn thì \(f'(x)\) là hàm số lẻ.b) Nếu \(f(x)\) là hàm số lẻ thì \(f'(x)\) là hàm số chẵn.
Đề: Cho parabol: $y = {x^2}+(2m + 1)x + {m^2} – 1$. Trong đó $m$ là tham số.a) Tìm quỹ tích đỉnh của parabol khi $m$ biến thiênb) Chứng minh rằng khoảng cách giữa các giao điểm của đường thẳng $y = x$ với parabol không phụ thuộc vào $m$.c) Chứng minh rằng với mọi giá trị của $m$, parabol luôn tiếp xúc với một đường thẳng cố định
Đề bài: Cho parabol: $y = {x^2}+(2m + 1)x + {m^2} - 1$. Trong đó $m$ là tham số.a) Tìm quỹ tích đỉnh của parabol khi $m$ biến thiênb) Chứng minh rằng khoảng cách giữa các giao điểm của đường thẳng $y = x$ với parabol không phụ thuộc vào $m$.c) Chứng minh rằng với mọi giá trị của $m$, parabol luôn tiếp xúc với một đường thẳng cố định Lời giải a) Tọa độ đỉnh của parabol … [Đọc thêm...] vềĐề: Cho parabol: $y = {x^2}+(2m + 1)x + {m^2} – 1$. Trong đó $m$ là tham số.a) Tìm quỹ tích đỉnh của parabol khi $m$ biến thiênb) Chứng minh rằng khoảng cách giữa các giao điểm của đường thẳng $y = x$ với parabol không phụ thuộc vào $m$.c) Chứng minh rằng với mọi giá trị của $m$, parabol luôn tiếp xúc với một đường thẳng cố định