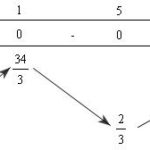
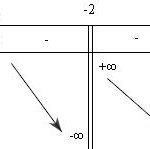
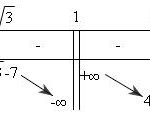
Đề bài: Giải hệ bất phương trình: $\left\{ \begin{array}{l}\log _2^2x - {\log _2}x^2 < 0\\\frac{x^3}{3} - 3x^2 + 5x + 9 > 0\end{array} \right.$ Lời giải ĐK :$x>0$$log_2^2x-log_2x^2$\Leftrightarrow 0Xét $f(x)=\frac{x^3}{3} -3x^2+5x+9$ thì $f^/(x)=x^2-6x+5$ $\Rightarrow f(x)>0 \forall x\in(1,4)$ Do đóHệ $\begin{cases}log_2^2x-log_2x^20 \end{cases} \Leftrightarrow 1 … [Đọc thêm...] vềĐề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}\log _2^2x – {\log _2}x^2 < 0\\\frac{x^3}{3} - 3x^2 + 5x + 9 > 0\end{array} \right.$
Bài tập Hàm số
Đề: Cho hàm số $y=\frac{x^{2}-mx+m-1}{x-2}$.Tìm $m$ để đồ thị hàm số nhận điểm $I(2;3)$ làm tâm đối xứng.
Đề bài: Cho hàm số $y=\frac{x^{2}-mx+m-1}{x-2}$.Tìm $m$ để đồ thị hàm số nhận điểm $I(2;3)$ làm tâm đối xứng. Lời giải Điểm $I(2;3)$ là tâm đối xứng của đồ thị khi với phép biến đổi tọa độ:$\begin{cases} X=x-2 \\ Y=y-3\end{cases} \Leftrightarrow \begin{cases} x=X+2 \\ y=Y+3\end{cases}$Hàm số sau là hàm lẻ:$Y+3=\frac{(X+2)^{2}-m(X+2)+m-1}{(X+2)-2}$Xét hàm … [Đọc thêm...] vềĐề: Cho hàm số $y=\frac{x^{2}-mx+m-1}{x-2}$.Tìm $m$ để đồ thị hàm số nhận điểm $I(2;3)$ làm tâm đối xứng.
Đề: Tìm:a) $GTNN:A=4+a^{2}b^{4}+a^{4}b^{2}-3 a^{2}b^{2} $b) $GTNN: B=x+y$ với $x,y>0$ và $\frac{2}{x}+\frac{3}{y}=6 $
Đề bài: Tìm:a) $GTNN:A=4+a^{2}b^{4}+a^{4}b^{2}-3 a^{2}b^{2} $b) $GTNN: B=x+y$ với $x,y>0$ và $\frac{2}{x}+\frac{3}{y}=6 $ Lời giải Thêm lời giải chi tiết … [Đọc thêm...] vềĐề: Tìm:a) $GTNN:A=4+a^{2}b^{4}+a^{4}b^{2}-3 a^{2}b^{2} $b) $GTNN: B=x+y$ với $x,y>0$ và $\frac{2}{x}+\frac{3}{y}=6 $
Đề: Xét hàm số với tham số $a:$ \(y = 2{x^3} + ax^2 – 12x – 13\) 1. Với những giá trị nào của $a$ thì đồ thị của hàm số có điểm cực đại và điểm cực tiểu và các điểm này cách đều trực tung?2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $a = 3.$
Đề bài: Xét hàm số với tham số $a:$ \(y = 2{x^3} + ax^2 - 12x - 13\) 1. Với những giá trị nào của $a$ thì đồ thị của hàm số có điểm cực đại và điểm cực tiểu và các điểm này cách đều trực tung?2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $a = 3.$ Lời giải $1$.Ta có \(y' = 6{x^2} + 2ax - 12\) luôn có hai nghiệm phân biệt \({x_{1,2}} = \frac{{ - a \pm \sqrt … [Đọc thêm...] vềĐề: Xét hàm số với tham số $a:$ \(y = 2{x^3} + ax^2 – 12x – 13\) 1. Với những giá trị nào của $a$ thì đồ thị của hàm số có điểm cực đại và điểm cực tiểu và các điểm này cách đều trực tung?2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $a = 3.$
Đề: Cho hàm số: $y = \frac{x^2 + mx – 2m – 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$.
Đề bài: Cho hàm số: $y = \frac{x^2 + mx - 2m - 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$. Lời giải $1.$ ĐK: $x … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{x^2 + mx – 2m – 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$.
Đề: Cho hàm số $y = f(x) = {x^4} + 2m{x^2} + m$, m là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =-1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $f(x) > 0$ với mọi $x$.Với các giá trị $m$ tìm được ở trên, chứng minh rằng hàm số :$F(x) = f(x) + f'(x) + f''(x) + f'''(x) + {f^{(4)}}x > 0 \forall x$$(f^{(4)} (x$) là kí hiệu đạo hàm cấp $4$ của hàm số $f(x)$ tại điểm $x)$
Đề bài: Cho hàm số $y = f(x) = {x^4} + 2m{x^2} + m$, m là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =-1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $f(x) > 0$ với mọi $x$.Với các giá trị $m$ tìm được ở trên, chứng minh rằng hàm số :$F(x) = f(x) + f'(x) + f''(x) + f'''(x) + {f^{(4)}}x > 0 \forall x$$(f^{(4)} (x$) là kí hiệu … [Đọc thêm...] vềĐề: Cho hàm số $y = f(x) = {x^4} + 2m{x^2} + m$, m là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =-1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $f(x) > 0$ với mọi $x$.Với các giá trị $m$ tìm được ở trên, chứng minh rằng hàm số :$F(x) = f(x) + f'(x) + f''(x) + f'''(x) + {f^{(4)}}x > 0 \forall x$$(f^{(4)} (x$) là kí hiệu đạo hàm cấp $4$ của hàm số $f(x)$ tại điểm $x)$
Đề: Cho hàm số:$y = \frac{ – 2x + 1}{x + 2}\,$$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. $2$. Viết phương trình tiếp tuyến với đồ thị hàm số song song với đường thẳng $y = -x$
Đề bài: Cho hàm số:$y = \frac{ - 2x + 1}{x + 2}\,$$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. $2$. Viết phương trình tiếp tuyến với đồ thị hàm số song song với đường thẳng $y = -x$ Lời giải $1.$ Xin dành cho bạn đọc. $2.$ Hoành độ tiếp điểm các tiếp tuyến song song với $y=-x$ là nghiệm của phương trình $f^/(x)=\frac{-3}{(x+1)^2} =-1\Leftrightarrow x=-1\pm … [Đọc thêm...] vềĐề: Cho hàm số:$y = \frac{ – 2x + 1}{x + 2}\,$$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. $2$. Viết phương trình tiếp tuyến với đồ thị hàm số song song với đường thẳng $y = -x$
Đề: Cho elip $(E): \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ với $F_1(-c;0)$. Tìm $M$ sao cho $MF_1$ ngắn nhất.
Đề bài: Cho elip $(E): \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ với $F_1(-c;0)$. Tìm $M$ sao cho $MF_1$ ngắn nhất. Lời giải Ta có: $MF_1=a+ex_M$ Mà $M \in (E) \Rightarrow -a \leq x_M \Rightarrow -ea \leq ex_M \Rightarrow a-ea \leq a+ex_M=MF_1$Do đó $MF_1$ ngắn nhất $\Leftrightarrow MF_1=a-\frac{c}{a}a=a-c \Leftrightarrow … [Đọc thêm...] vềĐề: Cho elip $(E): \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ với $F_1(-c;0)$. Tìm $M$ sao cho $MF_1$ ngắn nhất.
Đề: Cho hàm số $y=f(x)=2x^3-3(2m+1)x^2+6m(m+1)x+1 (1)$$a.$ Tìm quỹ tích điểm uốn.$b.$ Tìm quĩ tích điểm cực đại$c.$ Tìm quĩ tích trung điểm đoạn nối điểm cực đại và cực tiểu của đồ thị.
Đề bài: Cho hàm số $y=f(x)=2x^3-3(2m+1)x^2+6m(m+1)x+1 (1)$$a.$ Tìm quỹ tích điểm uốn.$b.$ Tìm quĩ tích điểm cực đại$c.$ Tìm quĩ tích trung điểm đoạn nối điểm cực đại và cực tiểu của đồ thị. Lời giải a. $ {\rm{y' }} = {\rm{ 6}}{{\rm{x}}^{\rm{2}}}{\rm{ - 6}}\left( {{\rm{2m }} + {\rm{ 1}}} \right){\rm{ x }} + {\rm{ 6m}}\left( {{\rm{m }} + {\rm{ 1}}} \right) $ $ … [Đọc thêm...] vềĐề: Cho hàm số $y=f(x)=2x^3-3(2m+1)x^2+6m(m+1)x+1 (1)$$a.$ Tìm quỹ tích điểm uốn.$b.$ Tìm quĩ tích điểm cực đại$c.$ Tìm quĩ tích trung điểm đoạn nối điểm cực đại và cực tiểu của đồ thị.
Đề: Cho hàm số: $y = \frac{2x^2 + 3x + 1}{x – 1}\,$$1$. Khảo sát và vẽ đồ thị hàm số trên.$2$. Một lớp học có $20$ học sinh, trong đó có $2$ cán bộ lớp. Hỏi có bao nhiêu cách cử $3$ người đi dự hội nghị Hội sinh viên của trường sao cho trong $3$ người có ít nhất một cán bộ lớp.
Đề bài: Cho hàm số: $y = \frac{2x^2 + 3x + 1}{x - 1}\,$$1$. Khảo sát và vẽ đồ thị hàm số trên.$2$. Một lớp học có $20$ học sinh, trong đó có $2$ cán bộ lớp. Hỏi có bao nhiêu cách cử $3$ người đi dự hội nghị Hội sinh viên của trường sao cho trong $3$ người có ít nhất một cán bộ lớp. Lời giải $1.$ $y= \frac{2x^2+3x+1}{x-1}=2x+5+\frac{6}{x-1} $* TXĐ: $D=R \setminus \left\{ … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{2x^2 + 3x + 1}{x – 1}\,$$1$. Khảo sát và vẽ đồ thị hàm số trên.$2$. Một lớp học có $20$ học sinh, trong đó có $2$ cán bộ lớp. Hỏi có bao nhiêu cách cử $3$ người đi dự hội nghị Hội sinh viên của trường sao cho trong $3$ người có ít nhất một cán bộ lớp.