
Đề bài: Cho hàm số: $y = \frac{x^2 + mx – 2m – 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$.
Lời giải
$1.$ ĐK: $x \ne – 2$
$(1)\Leftrightarrow (x – 2)m = y(x + 2) – x^2 + 4\,\, (2)$
Do đó A(x;y) sẽ là điểm cố định mà với mọi m, đồ thị hàm số ($1$) đều đi qua $\Leftrightarrow x \ne 2$ và ($2$) đúng $\forall m$
$ \Leftrightarrow \left\{ \begin{array}{l}
x – 2 = 0\\
y(x + 2) – {x^2} + 4 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = 0
\end{array} \right.$
Đồ thị luôn đi qua $A(2;0)$
$2.$ $y’ = \frac{{{x^2} + 4x + 4m + 4}}{{{{(x + 2)}^2}}}$
Hàm số đạt cực đại, cực tiểu $ \Leftrightarrow {x^2} + 4x + 4m + 4 = 0$ có $2$ nghiệm phân biệt.
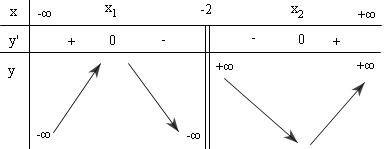
$ \Leftrightarrow \Delta ‘ = – 4m > 0 \Leftrightarrow m Với $m bảng biến thiên :
Điểm cực đại có tọa độ :
$\left\{ \begin{array}{l}
{x_1} = – 2 – \sqrt { – 4m} \,\,\,(3)\\
{y_1} = \frac{{x_1^2 + m{x_1} – 2m – 4}}{{{x_1} + 2}} = {x_1} – 2 + m + \frac{{ – 4m}}{{{x_1} +
2}}\,\,(4)
\end{array} \right.$
$(3)\Leftrightarrow \sqrt { – 4m} = – \left( {{x_1} + 2} \right) \Leftrightarrow \left\{ \begin{array}{l}
{x_1} – 4m = {\left( {{x_1} + 2} \right)^2}
\end{array} \right.$ thế vào ($4$) :
$\begin{array}{l}
\Rightarrow {y_1} = {x_1} – 2 – \frac{{{{\left( {{x_1} + 2} \right)}^2}}}{4} + \frac{{{{\left( {{x_1}
+ 2} \right)}^2}}}{{{x_1} + 2}} = 2{x_1} – \frac{{{{\left( {{x_1} + 2} \right)}^2}}}{4}\\
= – \frac{{x_1^2}}{4} + {x_1} – 1
\end{array}$
Vậy quỹ tích điểm cực đại là nửa Parabol với phương trình :
$\left\{ \begin{array}{l}
y = – \frac{{{x^2}}}{4} + x – 1\\
x \end{array} \right.$
$3.$ Xin dành cho bạn đọc.
