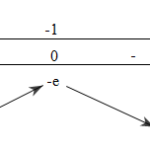
Đề bài: Tìm tập xác định của các hàm số:a) $y=\sqrt{3x+5}-\sqrt{3-2x}$ b) $y=\sqrt{3+5x}+\frac{2+x}{\sqrt{2x-3}}$ Lời giải a) $\sqrt{3x+5}$ xác định trên $D_{1}=\left \{ x\in R/3x+5\geq \left. 0 \right \} \right.=\left[ \begin{array}{l}-\frac{5}{3};+\infty \\\end{array} \right.)$$\sqrt{3-2x}$ xác định trên $D_{2}=\left \{ … [Đọc thêm...] vềĐề: Tìm tập xác định của các hàm số:a) $y=\sqrt{3x+5}-\sqrt{3-2x}$ b) $y=\sqrt{3+5x}+\frac{2+x}{\sqrt{2x-3}}$
Bài tập Hàm số
Đề: Tính vi phân của mỗi hàm số sau : a) $ y = 2 ^{-\frac{1}{\sin x}}$ b) $y = \ln \left [ \tan \left ( \frac{\pi}{2}-\frac{x}{4} \right ) \right ]$.
Đề bài: Tính vi phân của mỗi hàm số sau : a) $ y = 2 ^{-\frac{1}{\sin x}}$ b) $y = \ln \left [ \tan \left ( \frac{\pi}{2}-\frac{x}{4} \right ) \right ]$. Lời giải a) Ta có ngay : $dy = y'dx = \left ( 2^{-\frac{1}{\sin x} } \right ) dx = \left ( -\frac{1}{\sin x} \right )^' .2^{-\frac{1}{\sin x} }.\ln 2.dx $ $ = … [Đọc thêm...] vềĐề: Tính vi phân của mỗi hàm số sau : a) $ y = 2 ^{-\frac{1}{\sin x}}$ b) $y = \ln \left [ \tan \left ( \frac{\pi}{2}-\frac{x}{4} \right ) \right ]$.
Đề: Cho hàm số $f(x)=\frac{4^x}{4^x+2} $ Chứng minh rằng nếu $a+b=1$ thì $f(a)+f(b)=1$
Đề bài: Cho hàm số $f(x)=\frac{4^x}{4^x+2} $ Chứng minh rằng nếu $a+b=1$ thì $f(a)+f(b)=1$ Lời giải $f(a)+f(b)=\frac{4^a}{4^a+2}+ \frac{4^b}{4^b+2}=\frac{4^{a+b}+2.4^a+4^{a+b}+2+4^b}{(4^a+2)(4^b+2)}$$=\frac{2.4^1+2.4^a+2.4^b}{4^{a+b}+2.4^a+2.4^b+4} =\frac{2(4^a+4^b+4)}{2(4^a+4^b+4)}=1 $ … [Đọc thêm...] vềĐề: Cho hàm số $f(x)=\frac{4^x}{4^x+2} $ Chứng minh rằng nếu $a+b=1$ thì $f(a)+f(b)=1$
Đề: Cho hàm số: $y = \frac{2x^2 + kx + 2 – k}{x + k – 1}\,\,\,\,\,(1)$$1$. Khảo sát và vẽ đồ thị hàm số với $k = 0 (1).$$2$. Chứng minh rằng với mọi $k \ne 2$, đồ thị hàm số ($1$) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.$3$. Xác định $k$ để hàm số ($1$) đồng biến trên khoảng $(1; + \infty )$
Đề bài: Cho hàm số: $y = \frac{2x^2 + kx + 2 - k}{x + k - 1}\,\,\,\,\,(1)$$1$. Khảo sát và vẽ đồ thị hàm số với $k = 0 (1).$$2$. Chứng minh rằng với mọi $k \ne 2$, đồ thị hàm số ($1$) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.$3$. Xác định $k$ để hàm số ($1$) đồng biến trên khoảng $(1; + \infty )$ Lời giải $1.$ Xin dành cho bạn đọc. $2.$ Đồ thị qua … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{2x^2 + kx + 2 – k}{x + k – 1}\,\,\,\,\,(1)$$1$. Khảo sát và vẽ đồ thị hàm số với $k = 0 (1).$$2$. Chứng minh rằng với mọi $k \ne 2$, đồ thị hàm số ($1$) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.$3$. Xác định $k$ để hàm số ($1$) đồng biến trên khoảng $(1; + \infty )$
Đề: Cho hàm số $y=-\frac{1}{2}x^3+2x^2-3x+1 $. Viết phương trình tiếp tuyến của đồ thị $(C)$ của hàm số đó tại giao điểm của $(C)$ với trục tung
Đề bài: Cho hàm số $y=-\frac{1}{2}x^3+2x^2-3x+1 $. Viết phương trình tiếp tuyến của đồ thị $(C)$ của hàm số đó tại giao điểm của $(C)$ với trục tung Lời giải Giao điểm của $(C)$ và trục tung $A(0;1)$. Ta có: $y'=-x^2+4x-3$, suy ra hệ số góc tiếp tuyến tại $A$ là $y'(0)=-3$Phương trình tiếp tuyến của $(C)$ tại $A: y-1=-3(x-0)\Leftrightarrow y=-3x+1$ … [Đọc thêm...] vềĐề: Cho hàm số $y=-\frac{1}{2}x^3+2x^2-3x+1 $. Viết phương trình tiếp tuyến của đồ thị $(C)$ của hàm số đó tại giao điểm của $(C)$ với trục tung
Đề: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$
Đề bài: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$ Lời giải a) $y=f(x)=\frac{1}{x e^x}, x\in (-\infty ;0)$Ta có $f'(x)=-\frac{(x e^x)'}{(x e^x)^2}=-\frac{(1+x)e^x}{(x e^x)^2}=-\frac{1+x}{x^2 e^x} $$f'(x)=0 \Leftrightarrow x=-1\in (-\infty ;0).$Trên … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$
Đề: Tìm GTNN của: $y=\sqrt{ x^2-6x+18}+\sqrt{x^2+2x+2 }$
Đề bài: Tìm GTNN của: $y=\sqrt{ x^2-6x+18}+\sqrt{x^2+2x+2 }$ Lời giải Cần giải chi tiếtDùng tọa độ, đưa về tổng khoảng cách. … [Đọc thêm...] vềĐề: Tìm GTNN của: $y=\sqrt{ x^2-6x+18}+\sqrt{x^2+2x+2 }$
Đề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Đề bài: Cho hàm số \(y = - {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị. Lời giải $1$. Bạn đọc tự giải.$2$. Với \(m = 1\), có \(y = f\left( … [Đọc thêm...] vềĐề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Đề: Cho hàm số: $y = \frac{x^2 + (m – 2)x + m + 1}{x + 1}\,\,\,$$1.$ Khảo sát và vẽ đồ thị hàm số khi $m = 2.$$2.$ Tìm $m$ để trên đồ thị có hai điểm phân biệt $A, B$ sao cho :$\begin{array}{l} 5{x_A} – {y_A} + 3 = 0; 5{x_B} – {y_B} + 3 = 0\end{array}$Tìm $m$ để hai điểm $A, B$ đó đối xứng với nhau qua đường thẳng $(d)$ có phương trình: $x + 5y + 9 = 0$
Đề bài: Cho hàm số: $y = \frac{x^2 + (m - 2)x + m + 1}{x + 1}\,\,\,$$1.$ Khảo sát và vẽ đồ thị hàm số khi $m = 2.$$2.$ Tìm $m$ để trên đồ thị có hai điểm phân biệt $A, B$ sao cho :$\begin{array}{l} 5{x_A} - {y_A} + 3 = 0; 5{x_B} - {y_B} + 3 = 0\end{array}$Tìm $m$ để hai điểm $A, B$ đó đối xứng với nhau qua đường thẳng $(d)$ có phương trình: $x + 5y + 9 = 0$ Lời … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{x^2 + (m – 2)x + m + 1}{x + 1}\,\,\,$$1.$ Khảo sát và vẽ đồ thị hàm số khi $m = 2.$$2.$ Tìm $m$ để trên đồ thị có hai điểm phân biệt $A, B$ sao cho :$\begin{array}{l} 5{x_A} – {y_A} + 3 = 0; 5{x_B} – {y_B} + 3 = 0\end{array}$Tìm $m$ để hai điểm $A, B$ đó đối xứng với nhau qua đường thẳng $(d)$ có phương trình: $x + 5y + 9 = 0$
Đề: Cho hàm số \(y = \frac{{ – {x^2} + mx + m}}{{ – mx + m}}\)$1$. Tìm điểm cố định mà đồ thị hàm số đi qua với mọi $m$ \( \ne 0\)$2$. Viết phương trình đường thẳng đi qua điểm \(M\left( {0;\frac{5}{4}} \right)\) và tiếp xúc với đồ thị \(\left( {{C_1}} \right)\)
Đề bài: Cho hàm số \(y = \frac{{ - {x^2} + mx + m}}{{ - mx + m}}\)$1$. Tìm điểm cố định mà đồ thị hàm số đi qua với mọi $m$ \( \ne 0\)$2$. Viết phương trình đường thẳng đi qua điểm \(M\left( {0;\frac{5}{4}} \right)\) và tiếp xúc với đồ thị \(\left( {{C_1}} \right)\) Lời giải $1$. Ta có: \( \left\{ \begin{array}{l}- ymx + my = - {x^2} + mx + m\\mx \ne m\end{array} … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{ – {x^2} + mx + m}}{{ – mx + m}}\)$1$. Tìm điểm cố định mà đồ thị hàm số đi qua với mọi $m$ \( \ne 0\)$2$. Viết phương trình đường thẳng đi qua điểm \(M\left( {0;\frac{5}{4}} \right)\) và tiếp xúc với đồ thị \(\left( {{C_1}} \right)\)