Đề: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$

Đề bài: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$

Lời giải

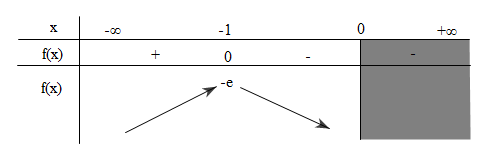
a) $y=f(x)=\frac{1}{x e^x}, x\in (-\infty ;0)$
Ta có $f'(x)=-\frac{(x e^x)’}{(x e^x)^2}=-\frac{(1+x)e^x}{(x e^x)^2}=-\frac{1+x}{x^2 e^x}  $
$f'(x)=0 \Leftrightarrow x=-1\in (-\infty ;0).$

Trên khoảng $(-\infty ;0)$, hàm số $y=f(x)$ có duy nhất một cực trị và cực trị này là cực đại.
Vậy, $\mathop {\max}\limits_{x\in(-\infty ;0) }f(x)=-e\Leftrightarrow x=-1$

b) Ta có $g'(x)=\frac{\ln x-\frac{1}{x}x }{(\ln x)^2}=\frac{\ln x-1}{(\ln x)^2}, x\in (1;+\infty )$
$g'(x)=0\Leftrightarrow \ln x=1\Leftrightarrow x=e.$ 
Bảng biến thiên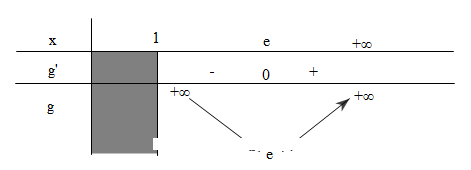

Vậy $\mathop {\min }\limits_{(1;+\infty )}g(x)=e\Leftrightarrow x=e $