
Đề bài: $1.$Khảo sát sự biến thiên và vẽ đồ thị hàm số:$y = \frac{x^2 – 2x + 2}{x – 1}$$2.$ Tìm giá trị lớn nhất và giá trị bé nhất của hàm số:$y = {\mathop{ sinx}} – cos^2x + \frac{1}{2}$
Lời giải
$1.$ * TXĐ: $R\setminus \left\{ {1} \right\} $
* Sự biến thiên:
$\mathop {\lim }\limits_{x \to +\infty } \frac{x^2-2x+2}{x-1} =\frac{x-2+\frac{2}{x} }{1-\frac{1}{x} }=+ \infty $
$\mathop {\lim }\limits_{x \to -\infty } \frac{x^2-2x+2}{x-1}=-\infty $
$\mathop {\lim }\limits_{x \to 1^+} \frac{x^2-2x+2}{x-1}=+\infty $
$\mathop {\lim }\limits_{x \to 1^-} \frac{x^2-2x+2}{x-1}=-\infty $
$\Rightarrow $ đồ thị nhận đường thẳng $x=1$ là Tiệm cận đứng.
$\mathop {\lim }\limits_{x \to +\infty }\left[ {y-(x-1)} \right]=\mathop {\lim }\limits_{x \to +\infty }\frac{1}{x-1}=0 $
$\mathop {\lim }\limits_{x \to -\infty }\left[ {y-(x-1)} \right]=\mathop {\lim }\limits_{x \to -\infty }\frac{1}{x-1}=0 $
$\Rightarrow $ đồ thị hàm số nhận đường thẳng $y=x-1$ làm tiệm cận xiên.
$y’=\frac{(2x-2)(x-1)-x^2+2x-2}{(x-1)^2}=\frac{x^2-2x}{(x-1)^2} $
$y’=0 \Leftrightarrow \left[ \begin{gathered} x=0 \\ x=2 \end{gathered} \right. $
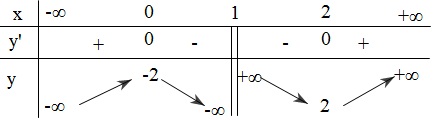
BBT:
Hàm số đồng biến trên $(-\infty ; 0) $ và $ (2; + \infty )$
Hàm số nghịch biến trên $(0;1)$ và $(1;2)$
Hàm số đạt cực đại tại $x=0, y_{CĐ}=-2$
Hàm số đạt cực tiểu tại $x=2, y_{CT}=2$
* Đồ thị:
Giao với Oy tại $(0;-2)$
Đồ thị hàm số nhận điểm $I(1;0)$ làm tâm đối xứng.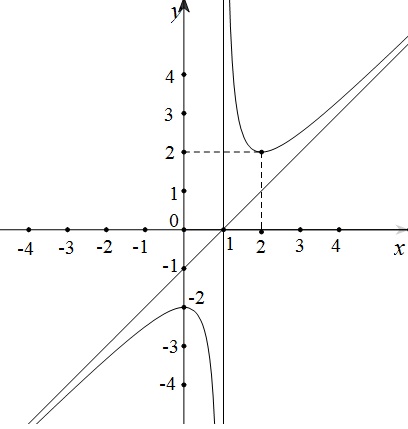
$2.$ Ta có $y=sinx+1-\sin ^2x-\frac{1}{2} =sin^2x+sinx-\frac{1}{2} $
Đặt $t=sinx$ thì $t\in[-1,1]$ và $y=t^2+t-\frac{1}{2} $ có $y^/(t)=2t+1$
Bảng biến thiên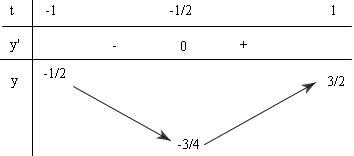
$\max y=\frac{3}{2} \Leftrightarrow t=1 \Rightarrow \sin x=1 \Leftrightarrow x=\frac{\pi }{2}+k2 \pi (k \in Z) $
$\min y=-\frac{3}{4} \Leftrightarrow t=-\frac{1}{2} \Rightarrow \sin x=-\frac{1}{2} \Leftrightarrow \left[ \begin{gathered} x=-\frac{\pi }{6}+k2 \pi \\ x=\frac{7 \pi }{6}+k2 \pi \end{gathered} \right.(k \in Z) $
